EDTA: Videos & Practice Problems

EDTA, a hexaprotic acid, can exist in multiple forms depending on the pH of the solution, influencing its ability to form metal complexes. The basic form of EDTA is most effective for complexation, with formation constants (K_f) indicating the stability of these complexes. The relationship between pH and the fraction of the basic form is crucial for determining the concentration of free metal ions. The conditional formation constant (K_f') incorporates the fraction of EDTA in its basic form, essential for understanding metal-ligand interactions.

EDTA

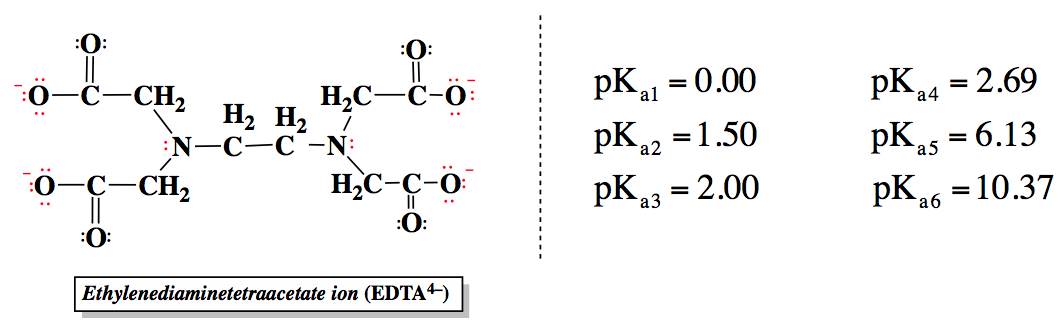
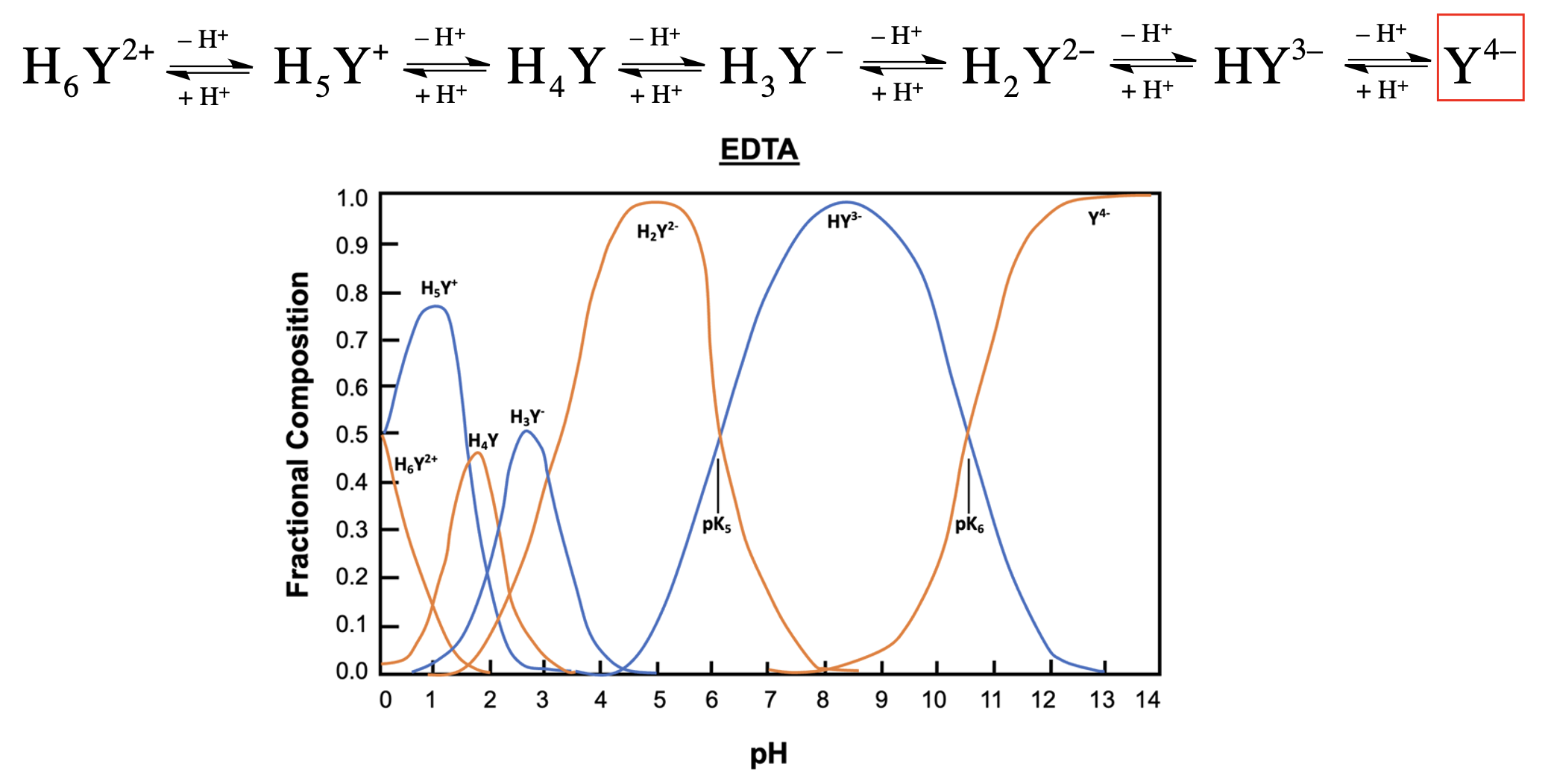
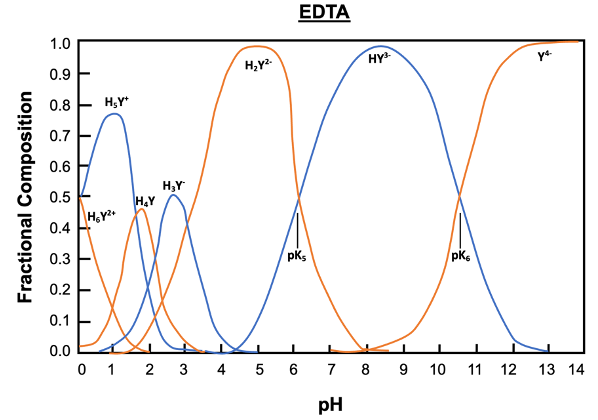
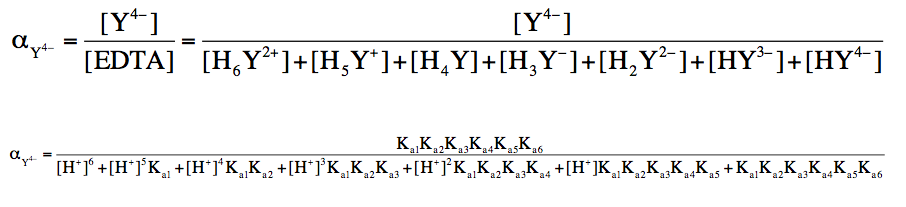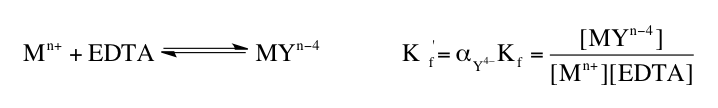EDTA, or ethylenediaminetetraacetic acid, is a versatile compound that can exist in multiple protonation states, depending on the pH of the solution. In its fully protonated form, EDTA is a hexaprotic acid, represented as H₆Y²⁺, indicating it can donate up to six protons. As the pH increases, protons are removed, leading to various deprotonated forms, with the fully deprotonated state being EDTA^4-.

EDTA contains four carboxylate groups and two amine groups, each contributing to its acidity and pKa values. Carboxylic acids are generally strong organic acids, with lower pKa values, while the amine groups have higher pKa values. The relationship between pH and pKa is crucial: if the pH is greater than the pKa, deprotonation occurs; if the pH is less, protonation takes place. This dynamic allows EDTA to adapt its charge based on the surrounding environment.

In total, EDTA can exist in up to seven different forms, influenced by the solution's pH. The fully protonated form is stable in acidic conditions, while the neutral form is preferred for long-term transport. The basic form, where all acidic protons are removed, is optimal for forming metal complexes. A graph illustrating the predominance of these forms at various pH levels shows that at a pH of 6, there is an equilibrium between two specific forms of EDTA, while at a pH above 10.37, the basic form becomes dominant.

To calculate the fraction of EDTA in its basic form, the following equation is used:

Fraction of Basic Form = \(\frac{[Basic \, Form]}{[EDTA]}\)

Here, [EDTA] refers to the total concentration of all seven forms. This equation can be further refined when the pH is known, as the concentration of hydrogen ions \([H^+]\) can be derived from the pH using the formula:

\([H^+] = 10^{-\text{pH}}\)

Additionally, the acid dissociation constant \(K_a\) is related to pKa by the equation:

\(K_a = 10^{-\text{pKa}}\)

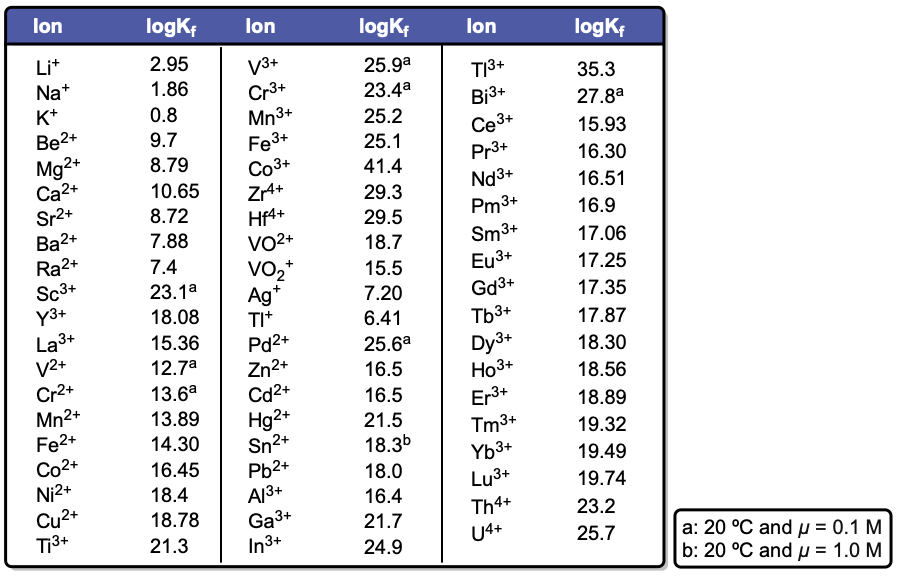
Understanding the various forms of EDTA and their dependence on pH is essential for effectively utilizing this compound in applications, particularly in metal complexation, where the basic form is most advantageous.

EDTA Calculations 1

To determine the concentration of the basic form of EDTA at a pH of 5.0, we start with the formal concentration of EDTA, which is 1.50 millimolar (mM). This can be converted to molarity (M) as follows: 1.50 mM = 1.50 × 10^-3 M. The concentration of the basic form of EDTA can be calculated using the equation:

[Basic Form] = [Total EDTA] × α

Here, α represents the fraction of EDTA that exists in the basic form at the specified pH. As pH increases, the fraction of EDTA in its basic form also increases, which is consistent with the behavior observed in the pH range from 0 to 14. At very high pH levels (around 13 to 14), nearly 100% of EDTA exists in the basic form.

At pH 5, we can look up the value of α for the basic form. After finding this value, we multiply it by the total concentration of EDTA to find the concentration of the basic form. For pH 5, the calculation yields:

[Basic Form] = 1.50 × 10^-3 M × α

Assuming α at pH 5 is approximately 2.90 × 10^-7, the concentration of the basic form becomes:

[Basic Form] = 1.50 × 10^-3 M × 2.90 × 10^-7 = 4.35 × 10^-10 M

This result indicates that out of the total concentration of 1.50 × 10^-3 M of EDTA, only 4.35 × 10^-10 M exists in the basic form at pH 5. This relationship highlights the importance of pH in determining the distribution of different forms of EDTA in solution, reinforcing the concept that as pH increases, the basic form becomes more predominant.

EDTA Calculations 1

To determine the fraction of EDTA that exists in its basic form at a pH of 8.50, we utilize a specific formula that incorporates the acid dissociation constants (Ka) of EDTA, which is a hexaprotic acid with six dissociation steps. The formula for the fraction of the basic form (α) is expressed as:

α = \(\frac{K_{a1} \cdot K_{a2} \cdot K_{a3} \cdot K_{a4} \cdot K_{a5} \cdot K_{a6}}{[H^+]^{6} + [H^+]^{5} \cdot K_{a1} + [H^+]^{4} \cdot K_{a1} \cdot K_{a2} + [H^+]^{3} \cdot K_{a1} \cdot K_{a2} \cdot K_{a3} + [H^+]^{2} \cdot K_{a1} \cdot K_{a2} \cdot K_{a3} \cdot K_{a4} + [H^+] \cdot K_{a1} \cdot K_{a2} \cdot K_{a3} \cdot K_{a4} \cdot K_{a5} + K_{a1} \cdot K_{a2} \cdot K_{a3} \cdot K_{a4} \cdot K_{a5} \cdot K_{a6}} \)

Given the pH, we can calculate the hydrogen ion concentration \([H^+]\) using the formula:

[H⁺] = \(10^{-pH}\) = \(10^{-8.50}\)

The provided pKa values for EDTA are as follows:

• pKa₁ = 0
• pKa₂ = 1.50
• pKa₃ = 2
• pKa₄ = 2.69
• pKa₅ = 6.13
• pKa₆ = 10.37

From these pKa values, we can derive the corresponding Ka values:

• K_a1 = \(10^{-0} = 1\)
• K_a2 = \(10^{-1.50} \approx 0.03162\)
• K_a3 = \(10^{-2} = 0.01\)
• K_a4 = \(10^{-2.69} \approx 0.00203\)
• K_a5 = \(10^{-6.13} \approx 7.41 \times 10^{-7}\)
• K_a6 = \(10^{-10.37} \approx 4.27 \times 10^{-11}\)

After calculating the Ka values, we substitute them into the formula for α. The calculations involve multiplying the Ka values and summing the contributions from each term in the denominator. The final result yields:

α ≈ 0.0133

This result indicates that approximately 1.33% of EDTA exists in its basic form at a pH of 8.50, which is consistent with the expected range of values between \(4.2 \times 10^{-3}\) and \(0.041\). As the pH increases, the fraction of the basic form of EDTA also increases. This method is specifically applicable when only the pH is provided. If the forms of EDTA were given, a different approach would be necessary to determine the fraction of the basic form.

Determine the pH where αY4– equals 0.20.

• A. pH ≈ 11.1
• B. pH ≈ 12.5
• C. pH ≈ 9.80
• D. pH ≈ 9.00

Answer: (C)

EDTA Complexes

Formation or stability constants are crucial in understanding the interactions between ligands, such as EDTA (ethylenediaminetetraacetic acid), and metal ions. These constants represent the equilibrium constant for the reaction where a ligand binds to a metal ion, denoted by the variable \( K_F \). In this context, the metal ion can have various charges, represented as \( M^{n+} \), where \( n \) can be 1, 2, 3, or 4, indicating the positive charge of the metal. The ligand EDTA is typically in its predominant form, \( Y^{4-} \), which allows it to effectively form complexes with metal ions.

When a metal ion combines with EDTA, it forms a complex, represented as \( [M(Y)]^{(n-4)} \). For example, when calcium ions (\( Ca^{2+} \)) react with EDTA, the overall charge of the complex is \( CaY^{2-} \), resulting in a net charge of -2. Conversely, when iron(III) ions (\( Fe^{3+} \)) react with EDTA, the complex \( [FeY]^{-1} \) has a net charge of -1. The formation of these complexes is reversible, establishing an equilibrium that can be described by the equation:

\[ K_F = \frac{[M(Y)]}{[M^{n+}][Y^{4-}]} \]

This equation is instrumental in determining the concentration of free metal ions in solution, as not all metal ions will bind with EDTA, leaving some in a free state. The formation constants for various metal-EDTA complexes vary, with higher positive charges on the metal leading to stronger interactions and higher \( K_F \) values. This indicates that as the charge of the metal increases, the affinity between the ligand and the metal also increases, favoring the formation of the EDTA complex.

Additionally, the pH of the solution significantly influences the form of EDTA present. At a pH of 13 or 14, the majority of EDTA exists in its basic form. However, at lower pH levels, other forms of EDTA become more prevalent. The conditional formation constant, denoted as \( K_F' \), can be used to assess the formation of the EDTA complex at any given pH. This constant is defined as:

\[ K_F' = \text{(fraction of EDTA in basic form)} \times K_F \]

Thus, the conditional formation constant can still be expressed in terms of the equilibrium concentrations:

\[ K_F' = \frac{[M(Y)]}{[M^{n+}][Y^{4-}]} \]

Understanding these concepts is essential for calculating the concentration of free metal ions, such as barium, in solutions where EDTA complexes are formed. By applying the appropriate equations and constants, one can effectively analyze the behavior of metal ions in the presence of ligands like EDTA.

EDTA Complexes

To determine the concentration of free barium ions in a solution where an EDTA complex has formed, we start by considering the reaction between barium ions (Ba²⁺) and EDTA, which has a charge of -4. The resulting complex can be represented as BaY^2-. Given an initial concentration of the barium EDTA complex at 0.10 M, we can set up an ICE (Initial, Change, Equilibrium) table to track the changes in concentration over time.

Initially, we have 0.10 M of the barium EDTA complex, and no initial amounts of free barium ions or EDTA. As the reaction progresses, the concentration of the complex decreases by an amount x, while the concentrations of free barium ions and EDTA increase by x. Thus, at equilibrium, the concentrations are represented as follows: [BaY] = 0.10 - x, [Ba²⁺] = x, and [EDTA] = x.

Next, we need to calculate the conditional formation constant (K_f) for the barium-EDTA complex. The conditional formation constant is influenced by the pH of the solution, which is given as 10. At this pH, the fraction of EDTA in its basic form is known to be 0.30. The stability constant (K_f) for barium ions is derived from its logarithmic value, log(K_f) = 7.88. To find K_f, we take the inverse of the logarithm: K_f = 10^7.88, which calculates to approximately 6.03 x 10⁷. Multiplying this by the fraction of EDTA gives us the conditional formation constant: K_f = 0.30 x 6.03 x 10⁷ = 2.28 x 10⁷.

Using the conditional formation constant, we can set up the equilibrium expression: K_f = [BaY] / ([Ba²⁺][EDTA]). Substituting the equilibrium concentrations into this expression yields:

2.28 x 10⁷ = (0.10 - x) / (x * x).

Rearranging this equation leads to:

2.28 x 10⁷ x² = 0.10 - x.

To solve for x, we rearrange it into a standard quadratic form:

2.28 x 10⁷ x² + x - 0.10 = 0.

Applying the quadratic formula, x = (-b ± √(b² - 4ac)) / 2a, where a = 2.28 x 10⁷, b = 1, and c = -0.10, we can find the values of x.

Calculating the discriminant and solving gives two potential values for x: 6.62 x 10^-5 M and -6.62 x 10^-5 M. Since concentrations cannot be negative, we discard the negative value. Thus, the concentration of free barium ions at equilibrium is 6.62 x 10^-5 M.

This process illustrates the importance of setting up an ICE table, understanding stoichiometric relationships, and calculating the conditional formation constant to determine the concentration of free metal ions in solution. The relationship between EDTA and the metal ion is crucial, as each mole of free metal ion reacts with one mole of EDTA to form the complex.

EDTA Complexes Calculations 1

To determine the conditional formation constant, denoted as \( K'_{f} \), for the EDTA complex at a pH of 8.0, we start by recognizing that \( K'_{f} \) is calculated using the equation:

\( K'_{f} = \alpha \times K_{f} \)

Here, \( \alpha \) represents the fraction of the basic form of EDTA. At a pH of 8.0, the fraction of the basic form of EDTA is given as \( 4.2 \times 10^{-3} \). This is derived from a reference chart that provides values for the basic form of EDTA at various pH levels.

In this scenario, we are dealing with the cobalt(III) ion, which has a charge of +3. The overall charge of the EDTA complex is -1, indicating that the EDTA molecule, which has a charge of -4, interacts with the cobalt(III) ion to form a stable complex.

Next, we need the stability constant \( K_{f} \) for the cobalt(III) ion. The logarithm of \( K_{f} \) is given as 41.4, so we can find \( K_{f} \) by using the inverse logarithm:

\( K_{f} = 10^{41.4} \)

Now, substituting the values into the equation for \( K'_{f} \):

\( K'_{f} = (4.2 \times 10^{-3}) \times (10^{41.4}) \)

Calculating this gives:

\( K'_{f} \approx 1.05 \times 10^{39} \)

This value indicates that the formation of the EDTA complex with cobalt(III) is highly favored, as \( K'_{f} \) is significantly greater than 1. A higher \( K'_{f} \) value suggests a strong tendency for the cobalt(III) ion to bind with EDTA, which is further enhanced by the positive charge of the metal ion. The greater the positive charge, the stronger the affinity of the EDTA ligand for the metal ion, leading to a more stable complex.

Understanding these concepts is crucial for analyzing metal-ligand interactions and predicting the stability of various complexes in solution.

EDTA Complexes Calculations 1

In this scenario, we are analyzing the equilibrium between free Tin(II) ions and a Potassium EDTA complex at a pH of 9.00. The Potassium ion acts as a spectator ion, while the EDTA complex can be represented as SnEDTA^2-. The relationship between the free Tin(II) ions and EDTA is crucial, as the formation of the complex can be expressed as:

Sn²⁺ + EDTA^4- ⇌ SnEDTA^2-

To solve for the concentration of free Tin(II) ions, we set up an ICE (Initial, Change, Equilibrium) table. Initially, we have 0.20 M of the Potassium EDTA complex, while the concentrations of free Tin(II) ions and EDTA are both 0. As the reaction progresses, the concentration of the complex decreases by x, while the concentrations of free Tin(II) ions and EDTA increase by x:

Initial: [Sn²⁺] = 0, [EDTA^4-] = 0, [SnEDTA^2-] = 0.20 M

Change: [Sn²⁺] = +x, [EDTA^4-] = +x, [SnEDTA^2-] = -x

Equilibrium: [Sn²⁺] = x, [EDTA^4-] = x, [SnEDTA^2-] = 0.20 - x

Next, we need to determine the conditional formation constant (K'_f) for the reaction. The formation constant (K_f) for the SnEDTA complex is given as 10^18.3. To find K'_f, we consider the pH and its effect on the equilibrium, resulting in K'_f = 0.041 × K_f.

Calculating K'_f gives us:

K'_f = 0.041 × 10^18.3 = 8.18 × 10¹⁶

We can now set up the equilibrium expression:

8.18 × 10¹⁶ = (0.20 - x) / x²

Multiplying both sides by x² leads to:

8.18 × 10¹⁶ x² = 0.20 - x

Rearranging gives us a quadratic equation:

8.18 × 10¹⁶ x² + x - 0.20 = 0

Using the quadratic formula, where a = 8.18 × 10¹⁶, b = 1, and c = -0.20, we find:

x = (-b ± √(b² - 4ac)) / 2a

Calculating the discriminant:

√(1² - 4 × 8.18 × 10¹⁶ × -0.20) = √(1 + 6.544 × 10¹⁷) ≈ 2.558 × 10⁸

Substituting back into the quadratic formula gives:

x = (-1 ± 2.558 × 10⁸) / (2 × 8.18 × 10¹⁶)

Calculating the positive root yields:

x ≈ 1.56 × 10^-9 M

This value represents the concentration of free Tin(II) ions at equilibrium. Therefore, the final concentration of free Tin(II) ions in the solution is:

[Sn²⁺] = 1.56 × 10^-9 M

Find the concentration of free Na ⁺ in 0.15 M Li ₃[Na(EDTA)] at pH = 10.00. 

• A. 0.024 M
• B. 0.13 M
• C. 0.063 M
• D. 0.22 M

Answer: (C)

Here’s what students ask on this topic:

What is EDTA and how does it function as a hexaprotic acid?

EDTA (Ethylenediaminetetraacetic acid) is a hexaprotic acid, meaning it can donate six protons (H⁺). In its fully protonated form, it is represented as H₆Y. The structure of EDTA includes four carboxylate groups and two amine groups, each with their own pKa values. The form of EDTA changes with the pH of the solution, affecting its protonation state. At low pH, EDTA is fully protonated, while at high pH, it is fully deprotonated, existing as Y^4-. This deprotonated form is most effective for forming metal complexes, as it can bind to metal ions through its multiple donor sites.

How does pH affect the different forms of EDTA?

The pH of a solution significantly affects the form of EDTA. At low pH (acidic conditions), EDTA is fully protonated (H₆Y). As the pH increases, protons are gradually removed, leading to forms like H₅Y^-, H₄Y^2-, and so on, until it reaches the fully deprotonated form Y^4- at high pH (basic conditions). The neutral form (H₂Y^2-) is often used for transport in solutions. The basic form (Y^4-) is ideal for forming metal complexes, as it can effectively bind to metal ions.

What are formation or stability constants (K_f) in the context of EDTA complexes?

Formation or stability constants (K_f) represent the equilibrium constant for the reaction between a ligand (like EDTA) and a metal ion. The general formula for this reaction is Mⁿ⁺ + Y^4- ⇌ MY^(n-4)-. The K_f value is calculated as the concentration of the EDTA-metal complex divided by the product of the concentrations of the free metal ion and EDTA. Higher K_f values indicate stronger and more stable complexes. The K_f values vary with the charge of the metal ion and the pH of the solution.

How do you calculate the fraction of EDTA in its basic form?

The fraction of EDTA in its basic form (Y^4-) can be calculated using the equation:

$\frac{{\alpha }_Y}{\mathrm{EDTA}}=\frac{{\mathrm{[Y]}}_{\mathrm{4-}}}{\mathrm{[EDTA]}}$

Here, [Y^4-] is the concentration of the basic form, and [EDTA] is the total concentration of all forms of EDTA. This can be expanded to include pH and pKa values, as:

$\frac{{\alpha }_Y}{\mathrm{EDTA}}=\frac{{\mathrm{[Y]}}_{\mathrm{4-}}}{\mathrm{[EDTA]}}=\frac{{\mathrm{[H]}}_{\mathrm{+}}{n}^{-}}{K_a}$

where n is the number of protons removed, and K_a values are the dissociation constants.

What is the conditional formation constant (K_f') for EDTA complexes?

The conditional formation constant (K_f') accounts for the fraction of EDTA in its basic form (Y^4-) at a given pH. It is calculated as:

$K_{\mathrm{f\text{'}}}={\alpha }_Y\times K_f$

Here, α_Y is the fraction of EDTA in its basic form, and K_f is the formation constant. This allows for the determination of the stability of EDTA-metal complexes at different pH levels, considering that not all EDTA will be in the Y^4- form at lower pH values.