So when we talk about entropy, we need to realize that entropy is closely related to the second law of thermodynamics. Now, this states that molecular systems tend to move spontaneously to a state of maximum randomness or disorder. So all of this is saying is when it comes to our total entropy, which is also our entropy of the universe, it is ever increasing. That means that the universe itself is becoming more and more chaotic. Universes or galaxies spin out of control. Their stars eventually explode, become, supernovas and eventually become black holes. The whole nature of the universe is one of degradation and breaking down into basically nothingness and chaos. I know it sounds a bit depressing but that's the general idea behind the second law. Everything moves to our universe or ΔS₁ otaù=ΔS₂ of our universe or ΔS₁ otaù=ΔS₂ of our system which is our chemical reaction plus ΔS₁ otaù=ΔS₂ of the surroundings. And together, following the second law of thermodynamics, this will always be greater than 0 because it's always increasing. Now, here, say, in terms of phase changes as well. This helps us determine what the sign will be for a particular process. Now here, if we take a look, we're going from a solid to a liquid to a gas. If we're going from a solid to a liquid, we say that that phase change is called melting or fusion. If we're going from a liquid to a gas, that's vaporization. Then we can go straight from a solid to a gas which is sublimation. In these processes, we're going to say the distance between molecules is increasing because remember, in a solid, the molecules are tightly held together. In a liquid, they're around each other but they're able to freely move around. In a gas, they're very spread apart. We're going to say here, we can see that we're going from a more ordered state to a less ordered state as we transition towards gases. As a result, we're going to say here that our entropy is increasing, so ΔS increases. In these processes, because they're all increasing my entropy, we see that ΔS's sign will be positive. Now, if we look at it the opposite way, if we're going from gas to liquid to solid, we're going to say here the distance between molecules is decreasing as they become more tightly packed as they transition to the solid state. In this case, we'd say that our entropy is decreasing. If our entropy is decreasing, that means that the sign of our entropy would have to be negative. Again, remember, entropy deals with chaos or disorder. The second law says that the natural processes or spontaneous process of the universe is to always increase our entropy. So ΔS₁ otaù will be greater than 0. Remember, in phase changes, you can have entropy equal to 0, but this is hard to come by. This is our third law of thermodynamics where the entropy is equal to 0 at absolute 0. The temperature would have to be 0 Kelvin. At 0 Kelvin, all motion stops within any given object and it's at that instance that the entropy of that object is exactly 0. Now, we're going to say here that this 0 Kelvin is highly theoretical. The average temperature of the universe itself is around 2 Kelvin. This 0 Kelvin is just a theoretical number. If we were able to get to that temperature, we assume that all motion would stop. But again, we haven't been able to get to that number so that's why it's highly theoretical. Now that we understand the basic generalities of entropy, we'll move on to the next video where we talk about comparing the entropies of different compounds to one another. Click on the next video and see how we approach comparisons of entropy.
Chemical Thermodynamics: Entropy - Online Tutor, Practice Problems & Exam Prep
Entropy represents the quantity of a system's thermal energy that couldn't be converted into mechanical work.
Understanding Entropy
Entropy
Video transcript
Entropy
Video transcript
So when we're taking a look at covalent compounds, we'll be able to compare their entropies to one another. Remember, covalent compounds are compounds composed of just non-metals bonded to one another. We're going to say here whenever you need to compare the entropies of covalent compounds, the guidelines below must be followed. What you do first is you have to compare their phases to one another. We're going to say here that gases, which have their molecules most spaced out, are the most entropic. After that, we have aqueous compounds. These are just compounds that are dissolved in some type of solvent, usually water, then we're going to say liquid which would be water, or some other type of liquid maybe hexane solvent, or methylene chloride solvent. Then we have finally solids. Now solids have their molecules most closely packed to one another, so they have the lowest entropy. That's why we can say as we go from gases to solids, the molecules become more organized and less chaotic and therefore less entropic.
Now, let's say your compounds that you're comparing are in the same phase. If so, we move on to the second criteria, which are microstates. Microstates are just the different ways a molecule can bend and orient itself, and they would have similar energies. Now, to make this simple, we're just going to connect microstates to complexity. Now, we're going to say here the more elements in the compound, then the more complex the compound, the higher its microstates, and therefore, the greater its entropy. For example, we're looking at NO2 gas versus NO3 gas. They're both covalent compounds. They both are gases, so we go to the criteria of microstates. Here, NO2 has in it 1 nitrogen and 2 oxygens for a total of 3 elements. NO3 has in it 1 nitrogen and 3 oxygens for a total of 4 elements. Because NO3 has more elements making it up, it has more complexity, therefore more microstates, therefore a greater entropy.
Now let's say that the covalent compounds you're comparing have the same phase, the same number of elements making them up, then we go to the final factors to look at in order to determine which one is more entropic. We look at their masses. We're going to say here the greater the mass, then the greater the entropy of that compound or element. For example, here we have xenon gas versus helium gas. Both are gases, both have the same complexities because they're just one element each, so we go to masses. Xenon weighs approximately 131 grams from the periodic table. Helium weighs approximately 4 grams from the periodic table. Because xenon weighs more, xenon would be more entropic. So remember, these are the guidelines we must follow in this exact order when comparing the entropies of different covalent compounds.
Click on to the entropies of different ionic compounds.
Entropy
Video transcript
Now, when comparing the entropies of different ionic compounds, we must utilize lattice energy. Remember that an ionic compound fundamentally is a positive ion called a cation connected to a negative ion called an anion. We're going to say here lattice energy represents the energy released when 1 mole of an ionic crystal or ionic compound is formed from its gaseous ions. Here, if we take a look, we have the application of this idea. We have the gaseous ions of sodium chloride solid. So here we have gaseous sodium ion combining with gaseous chloride ion and together they form solid sodium chloride.
Here, this gives us an entropy value of negative 787 kilojoules per mole. Remember, we're forming connections and bonds here, which means that it's an exothermic reaction. Remember exothermic reactions are bond-forming reactions, which is why the delta h value here is negative. Now here we can come up with a makeshift equation to help give us a numerical value to our lattice energy. This is just a way of us understanding how we can compare the values of 2 different ionic solids to one another or ionic crystals.
Here we're going to say lattice energy, also known as electrostatic energy, equals the absolute value of cation charge times anion charge divided by cation radius plus anion radius. To keep things even simpler, we're going to say that radius can be connected to the period number of the element. So for example, if we're looking at sodium chloride, we're gonna say here that sodium chloride is Na+Cl-. So the charge of cation 1 is plus 1 and the anion charge is -1 in absolute terms divided by cation radius. We're going to look at the periodic table and say that sodium is in period 3 or row 3, so we're going to say 3 here for its radius.
Again, this isn't the actual radius of the sodium ion, this is just a simplified way of looking at the periodic table to give us an estimate of values for lattice energy, which allows us to compare different ionic compounds. Plus anion radius, chloride is also in the 3rd row, so that's 3. So 16. If we were to compare this to another ionic compound, let's say we're looking at Barium oxide, this is comprised of Ba2+O2-. So here its lattice energy would be plus 2 times negative 2 in absolute terms, divided by barium in row 6, oxygen in row 2, so that would be 4 over 8 or 12. We see that barium oxide has the largest estimate for its lattice energy than sodium chloride.
So, barium oxide has a larger lattice energy. Now what does this do? Well, we're going to say the larger the lattice energy, then the stronger the ionic bond between the ions. So there's a stronger connection between the barium ion and oxide ion than there is between the sodium ion and the chloride ion. This is indicative of the larger lattice energy estimate that we have. Now, this results in a higher boiling point, higher melting point, and lower entropies. Okay. So the higher your lattice energy, the more true these statements are.
Now if we were to look at the periodic table itself, we can come up with a trend. We can say as we head towards the top right corner of the periodic table, we can say that your lattice energy will increase. So here we come up with this makeshift equation to give us a numeric estimate that we can use to compare different ionic compounds to each other. And here we have the periodic table where we can look at the overall trend of lattice energy as we head from the left side of the periodic table towards the top right of the periodic table. This causes an increase in our lattice energy.
Entropy Calculations
Entropy Calculations 1
Video transcript
Here for example, when we're asked to predict the sign of entropy for each of the following processes. For the first one, we have I2. It's at 90 degrees Celsius and 5.0 atmospheres of pressure. Then it transitions to a new temperature of 50 degrees Celsius and 10 atmospheres of pressure. We can see that the change, what changes are occurring. Our temperature goes from 90 degrees Celsius to 50 degrees Celsius. That tells us we have a drop in temperature. Then our pressure goes from 5 atmospheres to 10 atmospheres. So we have an increase in pressure. We have to think about what the sign of entropy would be here. Is entropy increasing therefore making it positive or is entropy decreasing therefore making it negative? Well, we can see that remember if our temperature is decreasing, what's happening to the molecules within any given substance? As the temperature is dropping, those molecules become less energetic and therefore huddle closer together making more bonds. Also, pressure. If you have these molecules in a closed container and you're increasing the pressure, you're forcing them to be closer to one another. This also supports the idea that the entropy is decreasing. Here, we'd say that our entropy would be negative. There'd be a decrease in my entropy. Also, you could say if your pressure is increasing that means your volume is decreasing. We didn't talk about volume here, but pressure and volume are related to one another and the fact that they're inversely proportional to each other. They're basically opposites. Whatever happens to one happens to the other.
Next, here we have ammonium chloride solid breaking up to give us hydrogen chloride as a gas plus ammonia gas. Now, we're going to say here you have one reactant that is split up into 2 or more products. What's happening, we're breaking bonds. We're causing an increase in our entropy or chaos. Δs here would have to be positive. There's an increase in entropy.
Finally, we have CH4 gas plus 2 O2 gas gives us CO2 gas plus 2 waters as a liquid. What we need to realize here is that what's going on. We have as a total 1 mole of gas plus another 2 so we have 3 moles of gas here. And then on the product side, we only have 1 mole of gas and we have 2 moles of liquid. Remember, gases have the most entropy. By converting those 3 moles of gas into just 1 mole of gas and now 2 moles of liquid, we've decreased our overall chaos or disorder. Entropy here would be negative. There's a decrease in my entropy. Just remember, are you helping to form bonds or are you helping to break bonds? This is important in understanding what the sign would be for your delta s value.
Now that you've seen this example, move on to the next. We haven't talked about this one yet. If you want, you can just skip straight to the second video and see how we approach this problem, or you can attempt to do it on your own. Guys, if you're going to do it on your own, attempt it. If you get stuck, don't worry. Just look at the next video.
Entropy Calculations 1
Video transcript
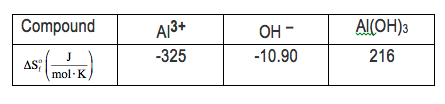
For this example, we haven't quite done questions like this yet, but let's give it a look. We're going to say when an aqueous solution containing aluminum ion at 25 degrees Celsius is mixed with an aqueous solution of hydroxide at 25 degrees Celsius, an immediate precipitate of insoluble aluminum hydroxide is formed. So in our equation, we have 1 mole of aluminum ion reacting with 3 moles of hydroxide ion to form 1 mole of aluminum hydroxide. Here, we're given the entropies of formation for each one of the compounds. So realize here that all compounds, all elements have an entropy greater than 0. The only way a compound or an element can have an entropy equal to 0 is if the temperature is at absolute 0. If the temperature is 0 Kelvin, each of them would have a delta S of formation equal to 0. As long as the temperature is above that, all the delta S values for formation will be greater than 0. Here, it asks us and the delta H of my reaction is negative 61.33 kilojoules per mole. They ask us to calculate the delta s total, for this reaction. Now remember, delta s total is related to delta s universe, which is part of our second law of thermodynamics. So delta s universe, which is the same thing as total, equals delta s of my reaction plus delta s of my surroundings. So we have to find both the reaction and surroundings, add them together to get our total. So here, we're going to start off by figuring out what delta s of reaction is. Now whether it's delta s of my reaction, delta f, delta g of my reaction, or delta h of my reaction, all of them equal products minus reactants. So we're going to use these entropies of formation values that were given to us. So here, our product is aluminum hydroxide. We have exactly 1 mole of it. So we're going to say here, 1 mole of aluminum hydroxide, which has an entropy of formation of 216 joules per mole kelvin minus my reactants. So we have 1 mole of aluminum ion. Each one is negative 325 joules per mole kelvin, plus 3 moles of hydroxide. Each one is negative 10.90 joules per mole kelvin. Here, my moles will cancel out. So my units here will be joules per kelvin. So here, when we do that, we're going to get 216 joules per kelvin minus a minus 357.7 joules per kelvin. So a minus of a minus really means you're adding. So that's going to come out to 573.7 joules per kelvin for my delta s of reaction. Now that we found that, we now figure out what our delta s of surroundings will be. Delta s of surroundings is equal to negative enthalpy of my reaction divided by my temperature in kelvin. The temperature we're told, is 25 degrees Celsius, so we just add 273.15 to that, which gives me 298.15 kelvin. So, 298.15 kelvin here on the bottom. And the enthalpy of our reaction is already given to us. We didn't have to calculate it. But if we did, they would give us the enthalpies of formation for each compound, and, again, you would just do products minus reactants in the same way you did the entropy of our reaction. Alright. So that's negative of a negative 61.33 kilojoules. So enthalpy of reaction usually is just in joules or kilojoules. You can drop the moles that we have there. So here, what we're going to have here, we're going to say here this going to give me a positive 0.205702 kilojoules per kelvin. But our entropy of reaction is in joules per kelvin, so we'll change this to joules. So 1 kilojoule is equal to 1000 joules. So that's 205.702 joules joules per kelvin. And then all we have to do now is add those two together. So delta s total, which is my delta s of reaction plus surroundings. That's 573.7 joules per kelvin plus 205.702 joules per kelvin. That's going to be approximately 779.402 joules per kelvin. Now, this answer, because our delta s total or universe is greater than 0, this tells us that this entire process is a spontaneous process. So, again, delta s total or universe is greater than 0. So by the second law of thermodynamics, this is a spontaneous process. So that's how we'd approach this problem. Now that you've seen example 12, attempt to do the practice question left here on the bottom. Once you do that, come back and see how I approach that same exact practice question.
Which of the following has the greatest entropy, S?
