Determine the interval(s) for which the function is continuous.
Table of contents
- 0. Functions4h 53m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation2h 18m
- 4. Derivatives of Exponential & Logarithmic Functions1h 16m
- 5. Applications of Derivatives2h 19m
- 6. Graphical Applications of Derivatives6h 0m
- 7. Antiderivatives & Indefinite Integrals48m
- 8. Definite Integrals4h 36m
- 9. Graphical Applications of Integrals1h 43m
- 10. Integrals of Inverse, Exponential, & Logarithmic Functions21m
- 11. Techniques of Integration2h 7m
- 12. Trigonometric Functions6h 54m
- Angles29m
- Trigonometric Functions on Right Triangles1h 8m
- Solving Right Triangles23m
- Trigonometric Functions on the Unit Circle1h 19m
- Graphs of Sine & Cosine46m
- Graphs of Other Trigonometric Functions32m
- Trigonometric Identities52m
- Derivatives of Trig Functions42m
- Integrals of Basic Trig Functions28m
- Integrals of Other Trig Functions10m
- 13: Intro to Differential Equations2h 23m
- 14. Sequences & Series2h 8m
- 15. Power Series2h 19m
- 16. Probability & Calculus45m
1. Limits and Continuity
Continuity
Multiple Choice
Determine the interval(s) for which the function is continuous.
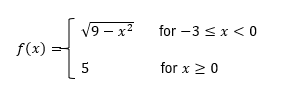
A
B
(−∞,0),[0,∞)
C
(−∞,∞)
D
The function is not continuous anywhere.
1 Comment
 Verified step by step guidance
Verified step by step guidance1
Step 1: Analyze the function piecewise. The function is defined as \( f(x) = \sqrt{9 - x^2} \) for \( -3 \leq x < 0 \), and \( f(x) = 5 \) for \( x \geq 0 \).
Step 2: Check the continuity of \( \sqrt{9 - x^2} \) on the interval \( -3 \leq x < 0 \). The square root function is continuous as long as the argument inside the square root is non-negative. Here, \( 9 - x^2 \geq 0 \) is satisfied for \( -3 \leq x \leq 3 \), so \( \sqrt{9 - x^2} \) is continuous on \( -3 \leq x < 0 \).
Step 3: Check the continuity of \( f(x) = 5 \) for \( x \geq 0 \). Since \( f(x) = 5 \) is a constant function, it is continuous for all \( x \geq 0 \).
Step 4: Examine the point \( x = 0 \), where the two pieces of the function meet. For \( x \to 0^- \), \( f(x) \to \sqrt{9 - 0^2} = 3 \). For \( x \to 0^+ \), \( f(x) = 5 \). Since the left-hand limit (3) does not equal the right-hand limit (5), the function is not continuous at \( x = 0 \).
Step 5: Combine the results. The function is continuous on \( [-3, 0) \) and \( [0, \infty) \), but not at \( x = 0 \). Therefore, the intervals of continuity are \( [-3, 0) \cup [0, \infty) \).
Related Videos
Related Practice
Multiple Choice
168
views
2
rank





