Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. Find two consecutive odd integers whose product is 143.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
The Square Root Property
Problem 3a
Textbook Question
Answer each question. Sides of a Right TriangleTo solve for the lengths of the right triangle sides, which equation is correct?
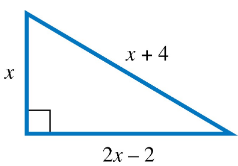
A. x^2=(2x-2)^2+(x+4)^2 B. x^2+(x+4)^2=(2x-2)^2 C. x^2=(2x-2)^2-(x+4)^2 D. x^2+(2x-2)^2=(x+4)^2
 Verified step by step guidance
Verified step by step guidance1
Identify the sides of the right triangle: the legs are labeled as \(x\) and \$3x - 3\(, and the hypotenuse is labeled as \)x + 9$.
Recall the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the legs. Mathematically, this is \(\text{hypotenuse}^2 = \text{leg}_1^2 + \text{leg}_2^2\).
Substitute the given side lengths into the Pythagorean theorem: \((x + 9)^2 = x^2 + (3x - 3)^2\).
This equation correctly relates the sides of the triangle according to the Pythagorean theorem.
Compare this equation to the options provided to determine which matches the correct form.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Pythagorean Theorem
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides. It is expressed as a² + b² = c², where c is the hypotenuse. This theorem is essential for relating the side lengths in right triangles.
Identifying the Hypotenuse
In a right triangle, the hypotenuse is the longest side and is opposite the right angle. Correctly identifying the hypotenuse is crucial because it is the side whose square equals the sum of the squares of the other two sides. In the given triangle, the side labeled 'x + 9' is the longest and thus the hypotenuse.
Recommended video:

Identifying Intervals of Unknown Behavior
Forming Equations from Triangle Sides
To solve for unknown side lengths, set up an equation using the Pythagorean theorem with the correct sides. Square the two shorter sides and sum them, then set this equal to the square of the hypotenuse. This equation can then be solved algebraically to find the value of x.
Recommended video:
Guided course

Standard Form of Line Equations

 6:12m
6:12mWatch next
Master Solving Quadratic Equations by the Square Root Property with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
46
views
