Transformations: Videos & Practice Problems

Transformations of functions include reflections, shifts, and stretches. Reflections occur when a graph is folded over an axis, changing the sign of the output values. Shifts involve moving the graph horizontally or vertically, represented by the equation f(x - h) + k, where h and k indicate the direction and magnitude of the shift. Stretches and shrinks modify the graph's shape based on constants multiplied inside or outside the function. Understanding these transformations is crucial for analyzing changes in domain and range, as they can significantly alter a function's behavior.

Intro to Transformations

Transformations of functions are essential concepts in mathematics that involve manipulating a function to change its position or shape. There are three primary types of transformations: reflections, shifts, and stretches. Understanding these transformations can simplify the study of functions significantly.

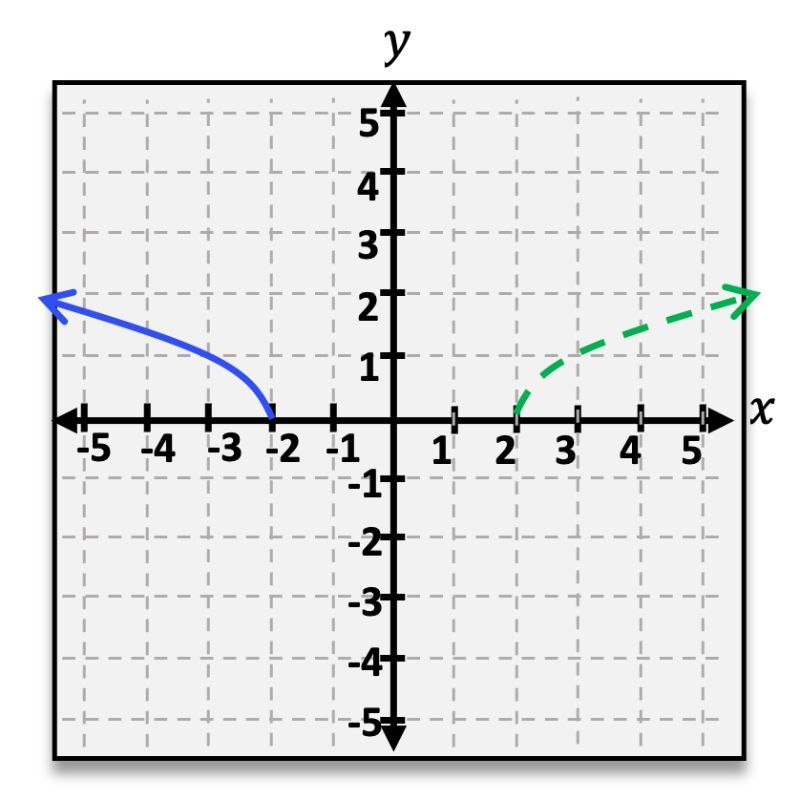
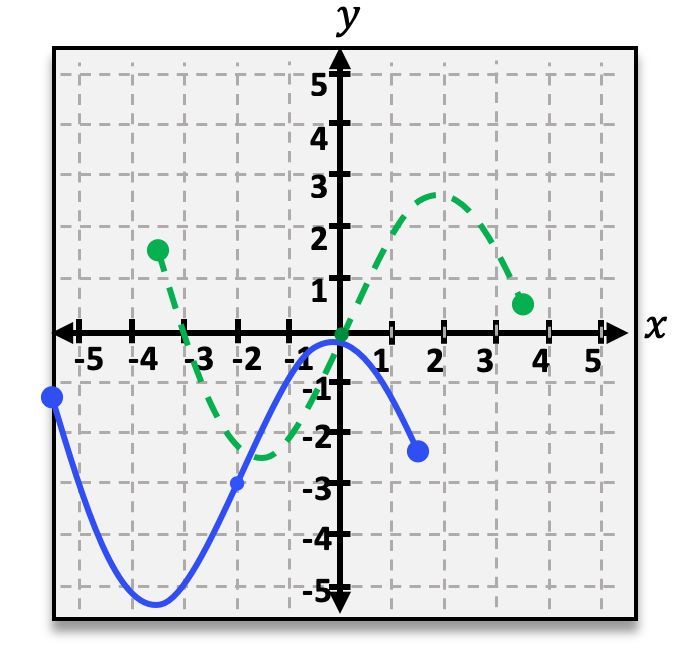
A reflection occurs when a function is flipped over a specific axis. For instance, reflecting a function over the x-axis changes its output to the negative of the original function, represented mathematically as f(x) → -f(x). This transformation effectively "folds" the graph over the axis.

A shift involves moving a function horizontally or vertically. The general form for a shift is f(x) - h + k, where h indicates the horizontal shift and k represents the vertical shift. For example, if a function is shifted right by 3 units and up by 2 units, it would be expressed as f(x - 3) + 2.

A stretch transformation occurs when a function is vertically stretched or compressed. This is represented by multiplying the function by a constant c, resulting in c * f(x). If c > 1, the function stretches vertically, while 0 < c < 1 compresses it.

To illustrate these transformations, consider the function f(x) = |x|. If we apply a shift transformation, such as P(x) = |x - 3| + 2, we can identify this as a shift to the right by 3 units and up by 2 units. This would correspond to a graph that has moved from the origin to a new position.

For a reflection, if we take Q(x) = -|x|, this represents a reflection over the x-axis, flipping the graph upside down. If we also have a stretch, such as R(x) = -2|x|, this indicates both a reflection and a vertical stretch, as the negative sign reflects the graph and the factor of 2 stretches it vertically.

In summary, understanding these transformations—reflections, shifts, and stretches—enables students to manipulate and analyze functions effectively. Recognizing how these transformations alter the function's graph is crucial for mastering function behavior in mathematics.

Reflections of Functions

Reflection transformations are a key concept in understanding how functions behave when their graphs are manipulated. A reflection occurs when a graph appears to be folded over a specific axis, resulting in a new orientation of the function. There are two primary types of reflections to consider: reflections over the x-axis and reflections over the y-axis.

When reflecting a graph over the x-axis, imagine creasing the graph at the x-axis and folding it down. This transformation changes the y-values of the function while keeping the x-values the same. Mathematically, this can be expressed as transforming the function f(x) into -f(x). For example, if a point on the graph is at (x, y), after the reflection, it will be at (x, -y). This means that positive y-values become negative, effectively flipping the graph upside down.

Conversely, reflecting a graph over the y-axis involves creasing the graph at the y-axis and folding it sideways. In this case, the y-values remain unchanged while the x-values are inverted. This transformation can be represented as changing f(x) to f(-x). For instance, a point at (x, y) will move to (-x, y) after the reflection, indicating that the graph is mirrored across the y-axis.

To illustrate these concepts, consider the function f(x) = x + 2. If we want to find the reflection of this function over the x-axis, we apply the transformation to get h(x) = -f(x) = - (x + 2) = -x - 2. This new equation represents the reflected function, which will have a graph that is the upside-down version of the original.

Understanding these transformations is crucial for graphing functions accurately and analyzing their behavior under various conditions. By mastering reflections, students can gain deeper insights into the properties of functions and their graphical representations.

Reflections of Functions Example 1

To understand the transformation of a function through reflection, consider the function \( f(x) \), represented by a curve. When we reflect this function over the x-axis, we create a new function \( g(x) \). This reflection can be visualized as folding the graph of \( f(x) \) along the x-axis, similar to how one would fold a sheet of paper.

Mathematically, reflecting a function over the x-axis involves negating the output values of the function. Therefore, the relationship between the original function and the reflected function can be expressed as:

\[ g(x) = -f(x) \]

In this transformation, every point on the graph of \( f(x) \) is mirrored across the x-axis. For instance, if a point on \( f(x) \) is at \( (a, b) \), after reflection, the corresponding point on \( g(x) \) will be at \( (a, -b) \). This means that any positive values of \( f(x) \) will become negative in \( g(x) \), and vice versa for negative values.

As you sketch the graph of \( g(x) \), visualize the original curve being flipped downwards for positive sections and upwards for negative sections. This transformation results in a new graph that maintains the same x-coordinates but alters the y-coordinates based on the reflection. Understanding this concept is crucial for mastering function transformations and their graphical representations.

Written below (green dotted curve) is a graph of the function $f\left(x\right)=\sqrt{x-2}$.If g(x) (blue solid curve) is a reflection of f(x) about the y-axis what is the equation for g(x)?

• A. $g\left(x\right)=\sqrt{-x-2}$
• B. $g\left(x\right)=\sqrt{-x}-2$
• C. $g\left(x\right)=\sqrt{x-2}$
• D. $g\left(x\right)=\sqrt{x}-2$

Answer: (A)

Shifts of Functions

Transformations of functions involve moving graphs either vertically or horizontally from their original positions. Understanding shifts is crucial, as they can be represented by specific notations that indicate how a function is altered. The general form for shifts can be expressed as f(x) \rightarrow f(x - h) + k, where h denotes the horizontal shift and k represents the vertical shift.

When considering vertical shifts, the graph moves up or down without changing the x-values. For instance, if a parabola is shifted from a position of 0 to 2, the y-values change by 2, indicating a vertical shift. In this case, the function transforms to f(x) + k, where a positive k results in an upward shift, while a negative k leads to a downward shift.

Conversely, horizontal shifts involve moving the graph left or right, affecting the x-values while keeping the y-values constant. For example, if a graph shifts from 0 to 3, the transformation can be represented as f(x - h), where a positive h indicates a shift to the right and a negative h indicates a shift to the left. This can be counterintuitive, as a negative sign in the equation suggests a rightward shift due to the nature of the transformation.

To illustrate these concepts, consider the transformation f(x - 2) + 3. Here, the h value is 2, indicating a shift 2 units to the right, while the k value is 3, indicating a shift 3 units up. Thus, the graph's new position reflects these transformations, maintaining its overall shape but relocating it based on the specified shifts.

Understanding these shifts is essential for graphing functions accurately and interpreting their transformations effectively. By mastering the notation and behavior of shifts, students can confidently manipulate and analyze various functions in mathematics.

The green dotted line in the graph below represents the function $f\left(x\right)$. The blue solid line represents the function $g\left(x\right)$, which is the function $f\left(x\right)$after it has gone through a shift transformation. Find the equation for $g\left(x\right)$.

• A. $g\left(x\right)=f\left(x-2\right)+3$
• B. $g\left(x\right)=f\left(x-2\right)-3$
• C. $g\left(x\right)=f\left(x+2\right)-3$
• D. $g\left(x\right)=f\left(x\right)-3$

Answer: (C)

Graphs of Shifted & Reflected Functions

In the study of function transformations, understanding how to graph shifted and reflected functions is essential. Transformations can include reflections, which involve flipping the graph over an axis, and shifts, which involve moving the graph to a different location on the coordinate plane. When combining these transformations, it’s important to recognize how they affect the function's equation and graph.

For instance, when reflecting a function over the x-axis, the function's output becomes negative. If we denote the original function as f(x), the reflected function can be expressed as -f(x). Shifting the graph involves adjusting the function's input or output. A horizontal shift to the left by h units is represented as f(x + h), while a vertical shift upwards by k units is represented as f(x) + k.

When combining these transformations, the order of operations matters. For example, if a function f(x) is first reflected over the x-axis and then shifted, the combined transformation can be expressed as:

g(x) = -f(x + h) + k

In a practical example, consider the absolute value function f(x) = |x|. If this function is reflected over the x-axis and then shifted 2 units to the left, the transformations can be calculated as follows:

1. Reflecting over the x-axis gives us -f(x) = -|x|.

2. Shifting 2 units to the left modifies the input to -f(x + 2) = -|x + 2|.

Thus, the final transformed function can be expressed as:

g(x) = -|x + 2|

By understanding these transformations and their notations, students can effectively graph and manipulate functions, making it easier to visualize complex transformations. This foundational knowledge is crucial for further studies in algebra and calculus.

Graphs of Shifted & Reflected Functions Example 1

To solve the problem involving the transformation of the function \( f(x) = x^3 \), we need to apply two specific transformations: a reflection over the x-axis and a vertical shift downward by 2 units. Understanding these transformations is crucial for deriving the new function \( h(x) \).

First, reflecting a function over the x-axis changes the function from \( f(x) \) to \( -f(x) \). Therefore, applying this transformation to our original function gives us:

\[ h_1(x) = -f(x) = -x^3 \]

Next, we need to account for the vertical shift downward by 2 units. A downward shift is represented by subtracting a value from the function. In this case, since we are shifting down 2 units, we subtract 2 from our already transformed function:

\[ h(x) = h_1(x) - 2 = -x^3 - 2 \]

Thus, the equation for the transformed function \( h(x) \) is:

\[ h(x) = -x^3 - 2 \]

Now, to sketch the graph of \( h(x) \), we start with the graph of the original function \( f(x) = x^3 \). The graph of \( x^3 \) is a cubic curve that passes through the origin and has a characteristic S-shape. After reflecting this graph over the x-axis, the curve will invert, resulting in a downward-opening S-shape. The next step is to shift this entire graph down by 2 units. This means every point on the graph of \( -x^3 \) will move down 2 units, resulting in the new center of the graph being at the point (0, -2).

In summary, the transformations yield the final function:

\[ h(x) = -x^3 - 2 \]

And the graph will reflect the characteristics of a cubic function, inverted and shifted down, centered at the point (0, -2).

Stretches & Shrinks of Functions

Transformations of functions are essential in understanding how graphs behave under various modifications. One key transformation is the stretch or shrink, which involves multiplying the function by a constant. This transformation can be categorized into vertical and horizontal stretches or shrinks, depending on where the constant is applied.

A vertical stretch occurs when a constant greater than 1 is multiplied outside the function, resulting in the graph being pulled away from the x-axis. Conversely, if the constant is between 0 and 1, it leads to a vertical shrink, compressing the graph towards the x-axis. For example, if we have a function f(x) and we multiply it by 2, the new function g(x) = 2f(x) will stretch the graph vertically by a factor of 2. If we multiply by 1/2, as in g(x) = (1/2)f(x), the graph will shrink vertically by half.

Horizontal stretches and shrinks are determined by constants multiplied inside the function. A constant between 0 and 1 results in a horizontal stretch, while a constant greater than 1 leads to a horizontal shrink. For instance, if we have g(x) = f(1/2x), this indicates a horizontal stretch because we effectively double the x-values to return to the original function. Conversely, if we have g(x) = f(2x), the graph will shrink horizontally, bringing points closer to the y-axis.

To summarize, the behavior of the graph under stretch and shrink transformations is dictated by the placement and value of the constant. Understanding these transformations allows for better manipulation and prediction of function graphs, which is crucial in various mathematical applications.

Stretches & Shrinks of Functions Example 1

In exploring the function \( f(x) = c \cdot x^2 \), we can analyze how different constants \( c \) affect the graph of the parabola. The general form of the parabola is represented by \( f(x) = x^2 \). When we substitute different values for \( c \), we observe distinct transformations in the graph.

First, consider the case where \( c = 2 \). The function becomes \( f(x) = 2 \cdot x^2 \). To understand the graph, we can evaluate specific \( x \) values:

• For \( x = 0 \): \[f(0) = 2 \cdot 0^2 = 0\]This gives us the point (0, 0).
• For \( x = -1 \): \[f(-1) = 2 \cdot (-1)^2 = 2 \cdot 1 = 2\]This results in the point (-1, 2).
• For \( x = 1 \): \[f(1) = 2 \cdot 1^2 = 2 \cdot 1 = 2\]This gives us the point (1, 2).

Thus, the graph of \( f(x) = 2 \cdot x^2 \) appears narrower than the standard parabola, indicating a horizontal shrink. This occurs because the constant \( c \) is greater than 1, which compresses the graph towards the y-axis.

Next, we analyze the case where \( c = \frac{1}{2} \). The function now is \( f(x) = \frac{1}{2} \cdot x^2 \). Evaluating this function at specific points yields:

• For \( x = 0 \): \[f(0) = \frac{1}{2} \cdot 0^2 = 0\]This again gives us the point (0, 0).
• For \( x = 2 \): \[f(2) = \frac{1}{2} \cdot 2^2 = \frac{1}{2} \cdot 4 = 2\]This results in the point (2, 2).
• For \( x = -2 \): \[f(-2) = \frac{1}{2} \cdot (-2)^2 = \frac{1}{2} \cdot 4 = 2\]This gives us the point (-2, 2).

The graph of \( f(x) = \frac{1}{2} \cdot x^2 \) appears wider than the standard parabola, indicating a horizontal stretch. This occurs because the constant \( c \) is between 0 and 1, which stretches the graph away from the y-axis.

It is important to note that these transformations can visually resemble vertical stretches or compressions. A horizontal shrink (when \( c > 1 \)) can appear similar to a vertical stretch, while a horizontal stretch (when \( 0 < c < 1 \)) can resemble a vertical compression. Understanding these relationships helps in visualizing the effects of different constants on the graph of a quadratic function.

Domain & Range of Transformed Functions

Transformations of functions, such as reflections, shifts, and stretches, can significantly alter the domain and range of a function. Understanding how to determine these changes is crucial for analyzing transformed functions effectively.

To find the domain and range of a transformed function, one can visualize the new graph after the transformation. For instance, consider a function f(x). If we compress the graph towards the x-axis, we can identify the domain by observing the horizontal extent of the graph. Similarly, compressing the graph towards the y-axis allows us to determine the range. For example, if the original function has a domain from -3 to 3 and a range from -3 to 3, a transformation that shifts the graph may result in a new domain from -2 to 4 and a range from -1 to 5, demonstrating that transformations can indeed modify both the domain and range.

Let’s explore a specific example with the function f(x) = x² and its transformation g(x) = (x - 3)² + 2. This transformation can be recognized as a shift, where h = 3 and k = 2. The positive value of h indicates a shift to the right, while the positive k indicates a shift upward. Thus, the vertex of the parabola shifts from the origin (0,0) to the point (3,2).

When analyzing the domain of g(x), we find that it remains all real numbers, or (−∞, ∞), since the parabola extends infinitely in both horizontal directions. However, the range changes due to the upward shift; the new range is from 2 to infinity, or [2, ∞), reflecting the lowest point of the transformed parabola.

This example illustrates that while the domain may remain unchanged, the range can be affected by transformations. Understanding these concepts is essential for effectively working with transformed functions in various mathematical contexts.

The green dotted curve below is a graph of the function $f\left(x\right)$. Find the domain and range of $g\left(x\right)$(the blue solid curve), which is a transformation of $f\left(x\right)$.

• A. Dom: $\left[1,4\right]$ , Ran: $\left[-5,-1\right]$
• B. Dom: $\left[1,5\right]$ , Ran: $\left[-5,1\right]$
• C. Dom: $\left[-1,3\right]$ , Ran: $\left[-2,4\right]$
• D. Dom: $\left[-2,3\right]$ , Ran: $\left[2,4\right]$

Answer: (B)

Here’s what students ask on this topic:

What are the three basic types of transformations in functions?

The three basic types of transformations in functions are reflections, shifts, and stretches. Reflections occur when a graph is folded over an axis, changing the sign of the output values. Shifts involve moving the graph horizontally or vertically, represented by the equation $f(x-h)+k$, where $h$ and $k$ indicate the direction and magnitude of the shift. Stretches and shrinks modify the graph's shape based on constants multiplied inside or outside the function. Understanding these transformations is crucial for analyzing changes in domain and range, as they can significantly alter a function's behavior.

How do you determine the new equation of a function after a reflection over the x-axis?

To determine the new equation of a function after a reflection over the x-axis, you multiply the entire function by -1. If the original function is $f\left(x\right)$, the reflected function will be $-f\left(x\right)$. This transformation changes the sign of all the output values, effectively flipping the graph over the x-axis. For example, if $f\left(x\right)=x^2$, the reflected function would be $-x^2$.

What is the difference between a vertical and a horizontal shift in a function?

A vertical shift in a function involves moving the graph up or down. This is represented by adding or subtracting a constant $k$ to the function, resulting in $f\left(x\right)+k$. A positive $k$ shifts the graph up, while a negative $k$ shifts it down. A horizontal shift involves moving the graph left or right. This is represented by modifying the input variable $x$ in the function, resulting in $f(x-h)$. A positive $h$ shifts the graph to the right, while a negative $h$ shifts it to the left.

How do you find the domain and range of a function after a transformation?

To find the domain and range of a function after a transformation, observe the new graph. For the domain, project the graph onto the x-axis and note the interval of x-values covered. For the range, project the graph onto the y-axis and note the interval of y-values covered. Transformations like shifts, reflections, and stretches can alter these intervals. For example, if a function $f\left(x\right)$ has a domain of $[-3,3]$ and a range of $[-3,3]$, a shift to the right by 2 units and up by 1 unit will change the domain to $[-1,5]$ and the range to $[-2,4]$.

What is the effect of a vertical stretch on a function's graph?

A vertical stretch on a function's graph occurs when a constant greater than 1 is multiplied outside the function. This transformation elongates the graph vertically, making it appear taller. For example, if the original function is $f\left(x\right)$ and the constant is $2$, the new function will be $2f\left(x\right)$. This means that every y-value of the original function is doubled, stretching the graph vertically. Conversely, if the constant is between 0 and 1, the graph undergoes a vertical shrink, making it appear shorter.