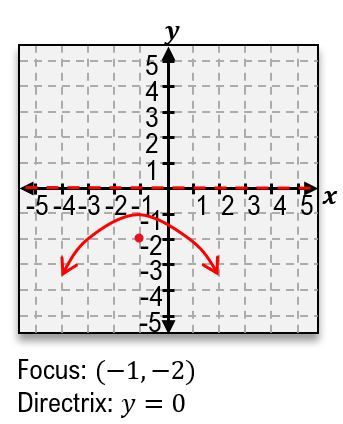
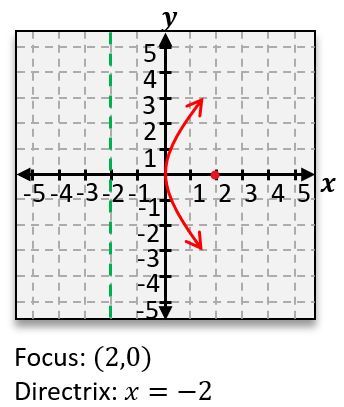
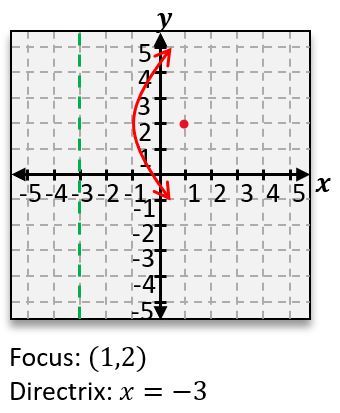
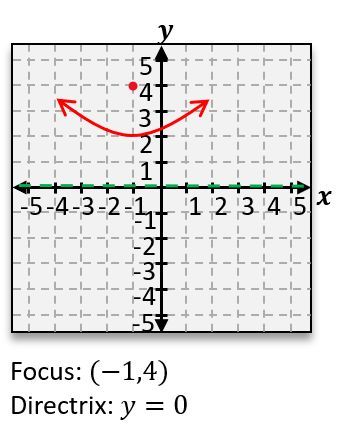
Conic sections are geometric shapes formed by slicing a three-dimensional cone with a two-dimensional plane. Understanding these shapes involves recognizing their unique characteristics and equations, which can be derived from the way the cone is intersected by the plane.
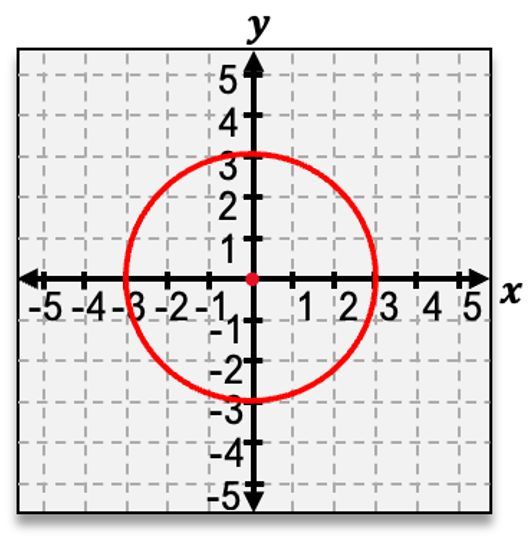
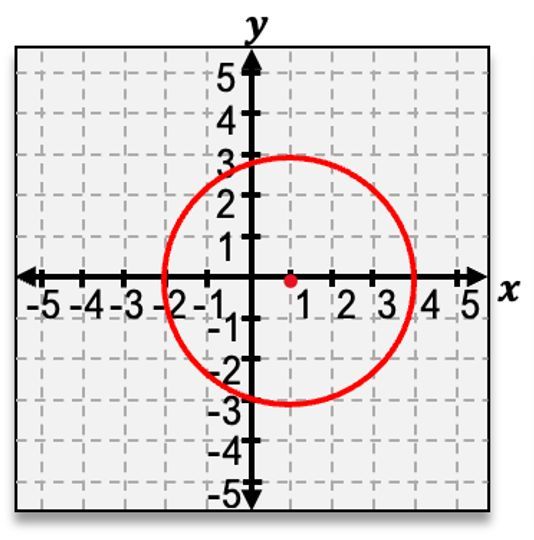
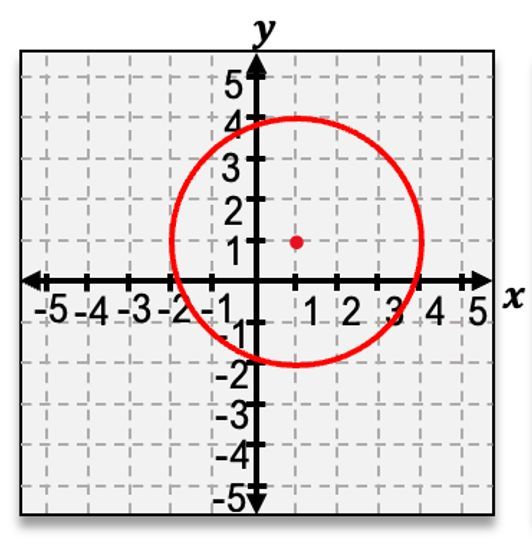
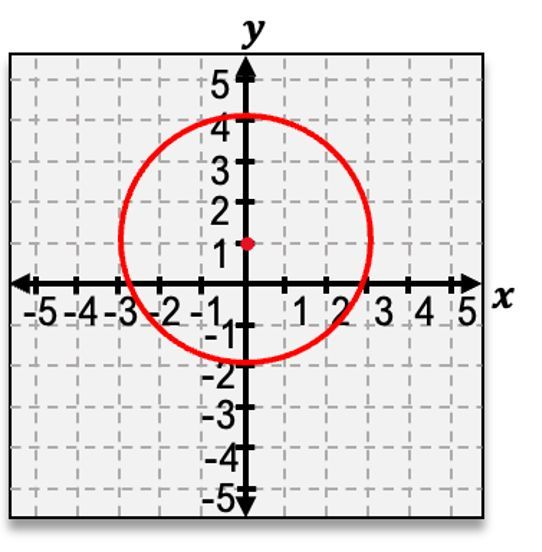
The first conic section is the circle, which is created when the cone is sliced horizontally. This results in a perfectly round shape, and the standard equation for a circle centered at the origin is given by:
\(x^2 + y^2 = r^2\)
where \(r\) is the radius of the circle.
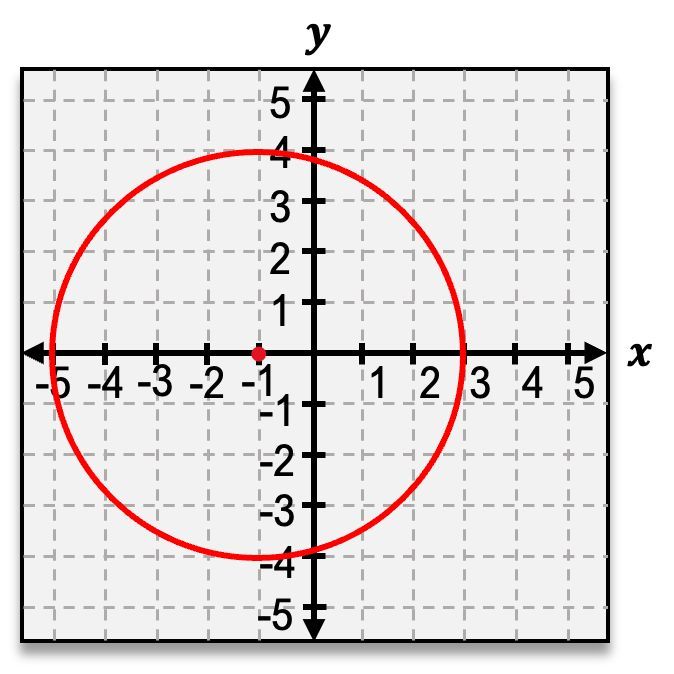
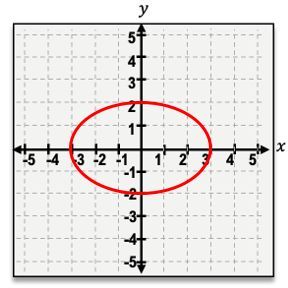
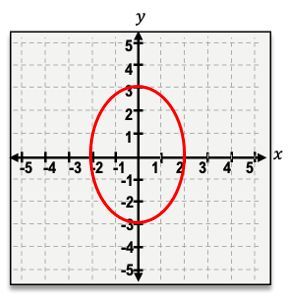
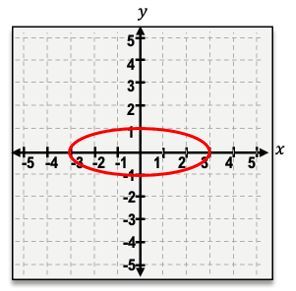
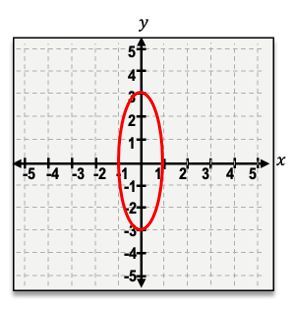
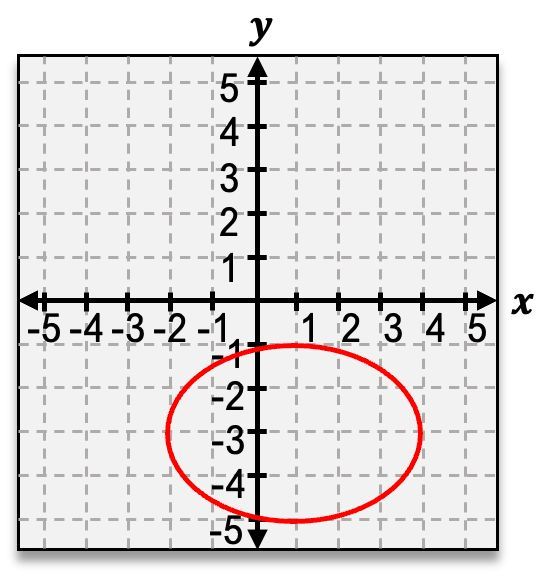
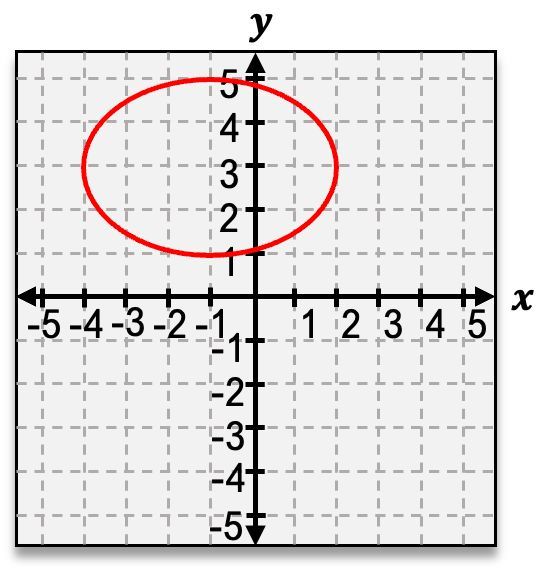
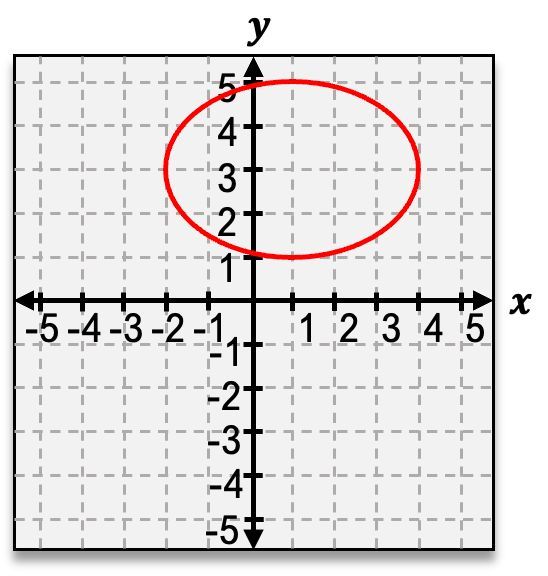
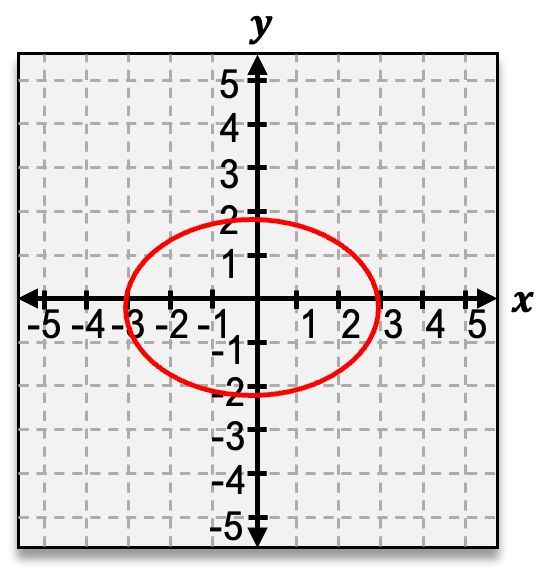
The second shape is the ellipse, which occurs when the cone is sliced at a slight angle. This results in an oval shape, resembling a stretched circle. The general equation for an ellipse centered at the origin is:
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)
where \(a\) and \(b\) are the semi-major and semi-minor axes, respectively.
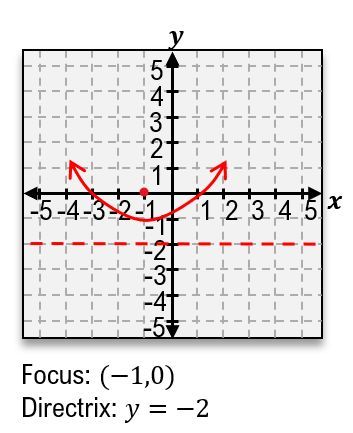
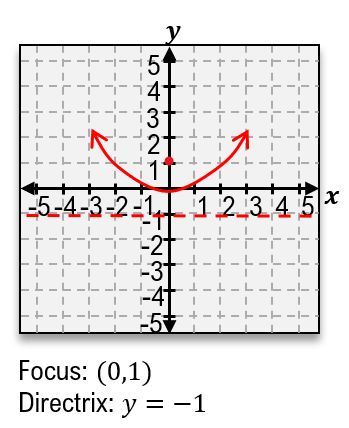
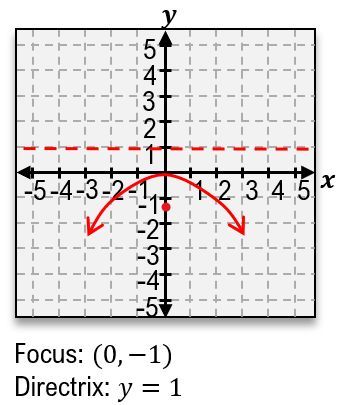
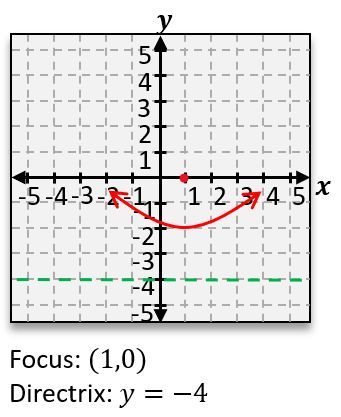
The parabola is formed when the plane is tilted at a steep angle, resulting in a U-shaped curve. The standard equation for a parabola that opens upwards is:
\(y = ax^2 + bx + c\)
where \(a\), \(b\), and \(c\) are constants that determine the shape and position of the parabola.
Finally, the hyperbola is created when the plane slices vertically through the cone, resulting in two separate curves that open away from each other. The standard equation for a hyperbola centered at the origin is:
\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)
where \(a\) and \(b\) define the distances from the center to the vertices and foci of the hyperbola.
Each of these conic sections has distinct properties and equations that are essential for solving related mathematical problems. By understanding how the shape is derived from the cone, students can better grasp the relationships between the different conic sections and their applications in various fields of study.