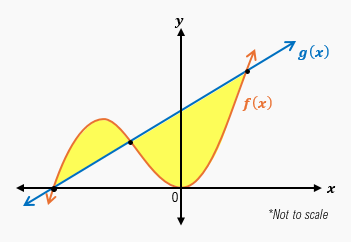
To find the area between two curves, we utilize the concept of definite integrals, which represent the area under a curve. When tasked with calculating the area between two functions, \( f(x) \) and \( g(x) \), over a specific interval, the process begins with graphing the functions and shading the area of interest. This visual representation helps clarify the relationship between the curves and the area to be calculated.
For example, consider the functions \( f(x) \) and \( g(x) \) defined on the interval from \( x = 0 \) to \( x = 1 \). To find the area between these curves, we first determine which function is on top and which is on the bottom within the specified interval. The area between the curves can be calculated by integrating the top function and subtracting the integral of the bottom function:
\[ \text{Area} = \int_{a}^{b} f(x) \, dx - \int_{a}^{b} g(x) \, dx \]
This can be combined into a single integral:
\[ \text{Area} = \int_{a}^{b} (f(x) - g(x)) \, dx \]
In our example, if \( f(x) = 4 - x^2 \) and \( g(x) = 2x + 1 \), we set up the integral from \( 0 \) to \( 1 \):
\[ \text{Area} = \int_{0}^{1} ((4 - x^2) - (2x + 1)) \, dx \]
After simplifying the integrand, we have:
\[ \text{Area} = \int_{0}^{1} (-x^2 - 2x + 3) \, dx \]
Next, we apply the power rule to find the antiderivative:
\[ \text{Antiderivative} = -\frac{1}{3}x^3 - x^2 + 3x \]
We evaluate this from \( 0 \) to \( 1 \):
\[ \text{Area} = \left[-\frac{1}{3}(1)^3 - (1)^2 + 3(1)\right] - \left[-\frac{1}{3}(0)^3 - (0)^2 + 3(0)\right] \]
Calculating this gives:
\[ \text{Area} = \left[-\frac{1}{3} - 1 + 3\right] - 0 = \frac{5}{3} \]
This result, \( \frac{5}{3} \), represents the area between the two curves over the interval from \( 0 \) to \( 1 \). It is important to note that this method is valid even if the functions are located below the x-axis, ensuring accurate area calculations regardless of the curves' positions.
As you continue to practice finding areas between curves, remember to visualize the functions, set up the integrals correctly, and apply the fundamental theorem of calculus to evaluate your results.






![Graph showing the area between two curves, f(x) in blue and g(x) in orange, highlighted in yellow on the interval [0,1].](https://static.studychannel.pearsonprd.tech/courses/calculus/thumbnails/eddf84c8-d1bf-4f07-899c-39929d63ad4b)