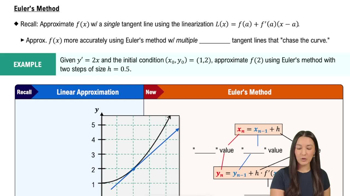
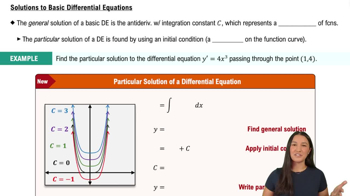
25. First-order chemical reactions In some chemical reactions, the rate at which the amount of a substance changes with time is proportional to the amount present. For the change of δ-gluconolactone into gluconic acid, for example,
dy/dt = -0.6y
when t is measured in hours. If there are 100 grams of δ-gluconolactone present when t=0, how many grams will be left after the first hour?