Use Euler’s method with a step size of to estimate the value of , where is the solution of the initial value problem
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
13. Intro to Differential Equations
Euler's Method
Problem 9.2.30a
Textbook Question
29–32. {Use of Tech} Errors in Euler’s method Consider the following initial value problems.
a. Find the approximations to y(0.2) and y(0.4) using Euler’s method with time steps of Δt = 0.2, 0.1, 0.05, and 0.025.
y′(t) = y/2, y(0) = 2; y(t) = 2eᵗᐟ²
 Verified step by step guidance
Verified step by step guidance1
Identify the differential equation and initial condition: \(y'(t) = \frac{y}{2}\) with \(y(0) = 2\). The exact solution is given as \(y(t) = 2e^{t/2}\), which will help us check the accuracy of Euler's method approximations.
Recall Euler's method formula for approximating the solution at discrete points: \(y_{n+1} = y_n + \Delta t \cdot f(t_n, y_n)\), where \(f(t, y) = \frac{y}{2}\) in this problem.
Set up the iterative process starting from \(t_0 = 0\) and \(y_0 = 2\). For each time step size \(\Delta t = 0.2, 0.1, 0.05, 0.025\), compute successive approximations \(y_1, y_2, \ldots\) until you reach \(t = 0.2\) and \(t = 0.4\).
For example, with \(\Delta t = 0.2\), calculate \(y_1\) at \(t_1 = 0.2\) using \(y_1 = y_0 + 0.2 \times \frac{y_0}{2}\), then calculate \(y_2\) at \(t_2 = 0.4\) similarly using \(y_1\). Repeat this process for the smaller step sizes, which will require more iterations.
Compare the approximations obtained for each \(\Delta t\) to observe how the step size affects the accuracy of Euler's method. Smaller \(\Delta t\) values generally yield better approximations to the exact solution \(y(t) = 2e^{t/2}\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Euler's Method
Euler's method is a numerical technique to approximate solutions of first-order differential equations using discrete steps. Starting from an initial value, it estimates the next value by moving along the slope given by the differential equation multiplied by the step size. Smaller step sizes generally improve accuracy but require more computations.
Recommended video:
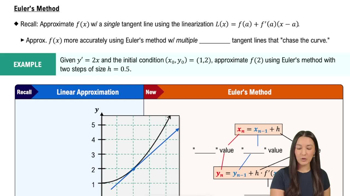
Euler's Method
Initial Value Problems (IVPs)
An initial value problem specifies a differential equation along with a starting point (initial condition) for the solution. The goal is to find the function that satisfies both the differential equation and the initial condition, which serves as the basis for numerical methods like Euler's method.
Recommended video:

Initial Value Problems
Error and Step Size in Numerical Methods
The error in Euler's method depends on the step size Δt; smaller steps reduce the local truncation error, leading to more accurate approximations. Understanding how step size affects error helps in balancing computational effort and solution precision when approximating values like y(0.2) and y(0.4).
Recommended video:

Euler's Method
Related Videos
Related Practice
Multiple Choice
165
views
1
rank


