Write a recursive formula for the geometric sequence .
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
14. Sequences & Series
Sequences
Problem 10.R.11a
Textbook Question
a.Does the sequence { k/(k + 1) } converge? Why or why not?
 Verified step by step guidance
Verified step by step guidance1
Identify the general term of the sequence, which is given by \(a_k = \frac{k}{k + 1}\).
Recall that to determine if a sequence converges, we need to find the limit of \(a_k\) as \(k\) approaches infinity, i.e., compute \(\lim_{k \to \infty} \frac{k}{k + 1}\).
To find this limit, divide the numerator and denominator by \(k\) to simplify the expression: \(\frac{k}{k + 1} = \frac{\frac{k}{k}}{\frac{k + 1}{k}} = \frac{1}{1 + \frac{1}{k}}\).
Evaluate the limit of the simplified expression as \(k\) approaches infinity: since \(\frac{1}{k} \to 0\), the expression approaches \(\frac{1}{1 + 0} = 1\).
Conclude that since the limit exists and equals 1, the sequence \(\left\{ \frac{k}{k + 1} \right\}\) converges, and its limit is 1.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Definition of a Sequence
A sequence is an ordered list of numbers defined by a specific formula for its terms. Understanding how each term is generated, such as k/(k + 1), is essential to analyze its behavior as k increases.
Recommended video:
Guided course
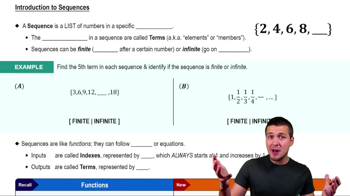
Introduction to Sequences
Limit of a Sequence
The limit of a sequence is the value that the terms approach as the index k goes to infinity. If the terms get arbitrarily close to a fixed number, the sequence converges to that limit.
Recommended video:
Guided course

Introduction to Sequences
Convergence Criteria
A sequence converges if its limit exists and is finite. To determine convergence, evaluate the limit of the general term as k approaches infinity and check if it approaches a specific number.
Recommended video:
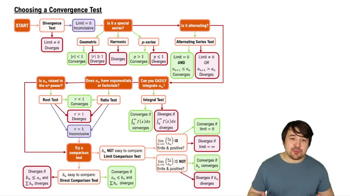
Choosing a Convergence Test
Related Videos
Related Practice
Multiple Choice
116
views
2
rank


