Graphing functions Use the guidelines of this section to make a complete graph of f.


f(x) = x² - 6x

Verified step by step guidance

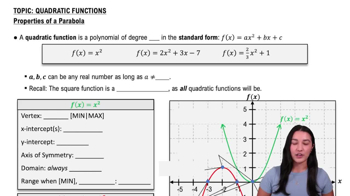
1. Identify the type of function: The function f(x) = x² - 6x is a quadratic function, which means its graph will be a parabola.
2. Find the vertex of the parabola: The vertex form of a quadratic function is f(x) = a(x-h)² + k, where (h, k) is the vertex. To find the vertex, use the formula h = -b/(2a) for the function f(x) = ax² + bx + c. Here, a = 1, b = -6, so h = -(-6)/(2*1) = 3. Substitute x = 3 into the function to find k: f(3) = 3² - 6*3 = -9. Thus, the vertex is (3, -9).
3. Determine the axis of symmetry: The axis of symmetry for a parabola is the vertical line that passes through the vertex. For this function, the axis of symmetry is x = 3.
4. Find the y-intercept: The y-intercept is the point where the graph intersects the y-axis, which occurs when x = 0. Substitute x = 0 into the function: f(0) = 0² - 6*0 = 0. So, the y-intercept is (0, 0).
5. Identify the direction of the parabola: Since the coefficient of x² (a = 1) is positive, the parabola opens upwards. This means the vertex is the minimum point of the graph.

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically expressed in the form f(x) = ax² + bx + c. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the sign of the coefficient 'a'. Understanding the general shape and properties of parabolas is essential for graphing quadratic functions.

Vertex of a Parabola

The vertex of a parabola is the highest or lowest point on the graph, depending on its orientation. For the quadratic function f(x) = x² - 6x, the vertex can be found using the formula x = -b/(2a), which gives the x-coordinate. The corresponding y-coordinate can be calculated by substituting this x-value back into the function, providing a key point for graphing.

Intercepts

Intercepts are points where the graph of a function crosses the axes. The x-intercepts occur where f(x) = 0, and can be found by solving the equation x² - 6x = 0. The y-intercept is found by evaluating f(0). Identifying these intercepts is crucial for accurately sketching the graph of the function.