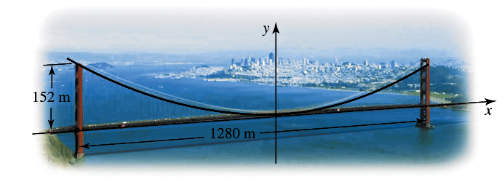
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
4x² - y² = 16