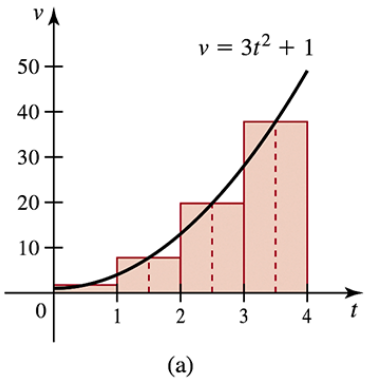
Approximating displacement The velocity in ft/s of an object moving along a line is given by v = 3t² + 1 on the interval 0 ≤ t ≤ 4, where t is measured in seconds.
(a) Divide the interval [0,4] into n = 4 subintervals, [0,1] , [1.2] , [2,3] , and [3,4]. On each subinterval, assume the object moves at a constant velocity equal to v evaluated at the midpoint of the subinterval, and use these approximations to estimate the displacement of the object on [0, 4] (see part (a) of the figure)

Verified step by step guidance

1. Divide the interval [0, 4] into 4 subintervals: [0, 1], [1, 2], [2, 3], and [3, 4]. The length of each subinterval is Δt = 1 second.
2. Find the midpoint of each subinterval: For [0, 1], the midpoint is t = 0.5; for [1, 2], the midpoint is t = 1.5; for [2, 3], the midpoint is t = 2.5; and for [3, 4], the midpoint is t = 3.5.
3. Evaluate the velocity function v(t) = 3t² + 1 at each midpoint: v(0.5), v(1.5), v(2.5), and v(3.5).
4. Approximate the displacement on each subinterval by multiplying the velocity at the midpoint by the subinterval length Δt. For example, the displacement on [0, 1] is approximately v(0.5) * Δt.
5. Add the displacements from all subintervals to estimate the total displacement of the object on [0, 4].

Key Concepts

Velocity Function

The velocity function describes how the speed of an object changes over time. In this case, the function v(t) = 3t² + 1 indicates that the velocity increases quadratically as time progresses. Understanding this function is crucial for determining the object's speed at any given moment within the specified interval.

Midpoint Rule

The Midpoint Rule is a numerical method used to approximate the integral of a function. By evaluating the function at the midpoint of each subinterval, we can estimate the area under the curve, which in this context represents the displacement of the object. This method provides a more accurate approximation than using the endpoints of the intervals.

Displacement

Displacement refers to the change in position of an object over a specific time interval. It can be calculated by integrating the velocity function over that interval. In this problem, estimating displacement involves summing the areas of rectangles formed by the velocity at midpoints of the subintervals, which approximates the total distance traveled by the object.