Basic Graphing of the Derivative: Videos & Practice Problems

Understanding the relationship between a function and its derivative is crucial in calculus. The derivative represents the slope of the tangent line at any point on the function's graph. When sketching the derivative, identify intervals where the function is increasing (positive derivative), decreasing (negative derivative), or flat (zero derivative). Special cases, such as sharp corners or discontinuities, indicate where the derivative does not exist. Recognizing these behaviors allows for efficient graphing of derivatives, enhancing comprehension of function dynamics.

Graphing The Derivative

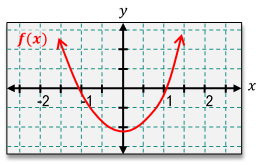
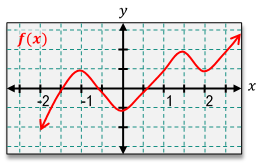
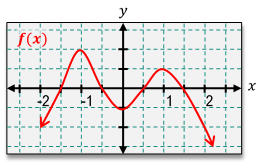
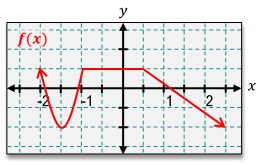
Understanding the relationship between a function and its derivative is crucial in calculus, particularly when analyzing the behavior of graphs. The derivative of a function, denoted as \( f'(x) \), represents the slope of the tangent line to the graph of the function \( f(x) \) at any given point. This means that if the function is increasing, the derivative is positive; if the function is decreasing, the derivative is negative; and if the function is flat (horizontal), the derivative is zero.

To sketch the derivative based on the graph of a function, one can follow a systematic approach. First, observe the behavior of the function as you move along the x-axis. For example, if you consider an interval where the function is increasing, the corresponding derivative will be above the x-axis, indicating positive values. Conversely, in intervals where the function is decreasing, the derivative will be below the x-axis, indicating negative values.

At points where the function has a horizontal tangent line, the derivative will equal zero. These points are critical as they represent local maxima or minima in the function. For instance, if a function has a peak or valley, the derivative will touch the x-axis at those points.

To illustrate this process, consider a function that increases from negative infinity to a certain point, then decreases, and finally increases again. The derivative can be sketched by marking the points where the derivative is zero (the peaks and valleys) and determining the intervals of positivity and negativity. For example, if the function increases from negative infinity to a point, the derivative will be positive in that interval. If it then decreases, the derivative will be negative until it reaches another point where it flattens out, indicating a zero derivative.

In summary, the key to sketching the derivative of a function lies in understanding the function's behavior across its domain. By identifying where the function is increasing, decreasing, or flat, one can effectively represent the derivative graphically. This method not only simplifies the process but also reinforces the fundamental concepts of calculus regarding the relationship between a function and its derivative.

Based on the graph of $f\left(x\right)$, describe the graph of the derivative $f^{\prime}\left(x\right)$ on the interval $\left(0,\infty\right)$.

• A. Below the x-axis
• B. Above the x-axis
• C. On the x-axis

Answer: (B)

Based on the graph of $f\left(x\right)$, describe the graph of the derivative $f^{\prime}\left(x\right)$at the point $x=-1$.

• A. Above the x-axis
• B. Below the x-axis
• C. On the x-axis

Answer: (C)

Based on the graph of $f\left(x\right)$, describe where the derivative curve $f^{\prime}\left(x\right)$ would be below the x-axis.

• A. (-$\infty$,-1) U (0,1)
• B. (-1,0) U (1,$\infty$)
• C. (-$\infty$, -1) U (1,$\infty$)
• D. (-1,1)

Answer: (B)

Graphing The Derivative Example 1

In this discussion, we explore how to sketch the derivative of a function, specifically focusing on a function that resembles a sine wave. To begin, understanding the behavior of tangent lines is crucial, as the derivative at any point corresponds to the slope of the tangent line at that point. The first step is to identify where the derivative is zero, which occurs at the peaks and valleys of the function where flat tangent lines can be drawn.

For a function oscillating like a sine wave, we can locate points where the slope is zero. These points will appear on the x-axis of the derivative graph. For instance, if we find a flat tangent line between -2 and -1, we can mark this point on the x-axis at approximately -1.5. Continuing this process, we identify additional points where the derivative crosses the x-axis.

Next, we analyze the behavior of the tangent lines as we move from left to right across the function. On the left side of a flat tangent line, the slopes are positive, indicating that the derivative will be above the x-axis. As we move right past this point, the slopes become negative, suggesting that the derivative will drop below the x-axis. This pattern continues, with the slopes gradually flattening out, indicating a transition back towards the x-axis.

As we sketch the derivative, we observe that the curve will rise and fall, reflecting the oscillatory nature of the original function. Notably, the resulting graph of the derivative resembles a cosine wave, which leads us to conclude that the derivative of a sine function is indeed a cosine function. This relationship highlights the interconnectedness of trigonometric functions and their derivatives.

In summary, by analyzing the slopes of tangent lines and their behavior across the function, we can effectively sketch the derivative, revealing the underlying relationships between sine and cosine functions. This method not only aids in visualizing derivatives but also reinforces the fundamental concepts of calculus.

Graphing The Derivative - Special Cases

Understanding how to graph the derivative of a function is essential, especially when dealing with special cases that may not present as smooth curves. These special cases often include sharp turns and jumps, which can complicate the process of determining the derivative. However, the approach remains fundamentally similar to that of regular functions, with a few additional rules to keep in mind.

When graphing the derivative, visualize a person walking along the graph from left to right. For sections of the graph that are horizontal, the derivative is zero, indicating that the slope is flat. This means that the corresponding portion of the derivative graph will lie along the x-axis. Conversely, if the graph is decreasing, the derivative will be negative, placing it below the x-axis. In cases where the graph is a straight line, the slope remains constant, resulting in a constant value for the derivative.

One critical aspect to remember is how to handle sharp corners or discontinuities. At these points, the derivative does not exist, which is represented by a jump or hole in the derivative graph. For example, if there is a sharp turn at a specific x-value, the derivative graph will reflect this by having a gap at that point, indicating that the slope cannot be defined there.

As you continue to analyze the graph, observe how the tangent lines behave. If the graph is increasing, the derivative will be positive and above the x-axis. The steepness of the tangent lines will affect the value of the derivative; flatter sections correspond to values closer to zero, while steeper sections yield higher values. Again, if there is a jump or discontinuity, the derivative will not exist at that point, resulting in another gap in the graph.

In summary, when sketching the derivative of a function, always consider the behavior of the original function. Remember that horizontal lines yield a derivative of zero, decreasing sections result in negative values, and sharp corners or jumps indicate that the derivative does not exist. By applying these principles, you can effectively graph the derivative even in the presence of special cases.

Based on the graph $f\left(x\right)$, describe all points where the derivative $f^{\prime}\left(x\right)$would have a jump.

• A. $x=-1.5$, $x=-1$, and $x=0.5$
• B. $x=-1$ and $x=0.5$
• C. $x=-1.5$
• D. Derivative $f^{\prime}\left(x\right)$ has no jumps

Answer: (B)

Graphing The Derivative - Special Cases Example 2

To sketch the derivative of a function, it is essential to identify where the tangent lines to the curve are flat, indicating a slope of zero. These points occur at peaks and valleys of the original function. For instance, if a peak is located at \( x = -1.5 \), the derivative \( f'(x) \) will touch the x-axis at this point. Additionally, if there is a continuous flat section of the graph from \( x = -1 \) to \( x = 1.5 \), the derivative will also remain on the x-axis throughout this interval.

As you analyze the graph from left to right, observe that in regions where the tangent lines have a positive slope, the derivative will be above the x-axis. Conversely, in sections where the tangent lines slope downwards, the derivative will be below the x-axis. This behavior allows for the construction of a continuous line segment for the derivative in these regions.

When encountering sharp corners in the original function, such as at points where the slope changes abruptly, it indicates a jump discontinuity in the derivative. At these points, an open circle should be placed on the derivative graph to signify that the derivative does not exist at that specific value.

Finally, if the original function has a linear section with a constant slope, the derivative will also be a constant value, resulting in a horizontal line on the derivative graph. This understanding of how to interpret the original function's features—such as peaks, valleys, and linear segments—enables the accurate sketching of its derivative.

Here’s what students ask on this topic:

How do you sketch the derivative of a function from its graph?

To sketch the derivative of a function from its graph, follow these steps: First, identify intervals where the function is increasing, decreasing, or flat. The derivative is positive where the function is increasing, negative where it is decreasing, and zero where it is flat. Next, locate points where the function has horizontal tangent lines (peaks and valleys) as these correspond to zero derivative values. Finally, consider any sharp corners or discontinuities, as the derivative does not exist at these points. Plot these observations on a new graph to sketch the derivative.

What does it mean when the derivative of a function is zero?

When the derivative of a function is zero, it means that the slope of the tangent line at that point is horizontal. In other words, the function is neither increasing nor decreasing at that specific point. This typically occurs at local maxima, minima, or points of inflection. On the graph of the function, these points appear as peaks, valleys, or flat regions. Identifying these points is crucial when sketching the derivative of a function.

How do sharp corners or discontinuities affect the derivative of a function?

Sharp corners or discontinuities in a function indicate points where the derivative does not exist. At a sharp corner, the function has an abrupt change in direction, making it impossible to define a single tangent line. Similarly, at a discontinuity, the function has a break or jump, preventing the derivative from being defined. When sketching the derivative, these points are represented by holes or jumps in the graph of the derivative, indicating that the derivative is undefined at those locations.

What is the relationship between the slope of a tangent line and the derivative of a function?

The slope of a tangent line to a function at a given point is the value of the derivative of the function at that point. The derivative represents the rate of change of the function, and the tangent line provides a linear approximation of the function's behavior near that point. A positive slope indicates an increasing function, a negative slope indicates a decreasing function, and a zero slope indicates a flat or stationary point. Understanding this relationship is key to interpreting and sketching the derivative of a function.

How can you determine if the derivative of a function is positive or negative?

To determine if the derivative of a function is positive or negative, observe the behavior of the function's graph. If the function is increasing (moving uphill) over an interval, the derivative is positive in that interval. Conversely, if the function is decreasing (moving downhill), the derivative is negative. By analyzing the slope of the tangent lines at various points on the graph, you can identify where the derivative is positive, negative, or zero, which helps in sketching the derivative accurately.