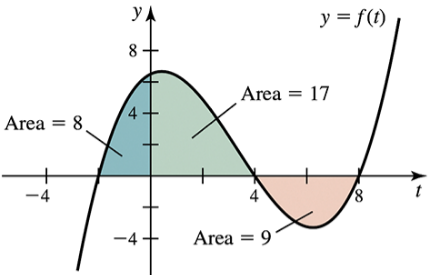
Determine the area of the shaded region in the following figures.
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
9. Graphical Applications of Integrals
Area Between Curves
Problem 5.3.13a
Textbook Question
Area functions The graph of ƒ is shown in the figure. Let A(x) = ∫₋₂ˣ ƒ(t) dt and F(x) = ∫₄ˣ ƒ(t) dt be two area functions for ƒ. Evaluate the following area functions.
(a) A (―2)
 Verified step by step guidance
Verified step by step guidance1
Understand the problem: We are tasked with evaluating A(-2), where A(x) = ∫₋₂ˣ ƒ(t) dt. This means we need to calculate the definite integral of the function ƒ(t) from -2 to -2.
Recall the property of definite integrals: If the upper and lower limits of the integral are the same, the integral evaluates to 0. Mathematically, ∫ₐₐ ƒ(t) dt = 0.
Apply this property to A(-2): Since the limits of integration are both -2, the integral evaluates to 0.
Conclude that A(-2) = 0 based on the property of definite integrals.
No further calculations are needed as the result is determined by the fundamental property of definite integrals.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Definite Integral
A definite integral represents the signed area under a curve between two points on the x-axis. It is calculated using the integral symbol and limits of integration, providing a numerical value that corresponds to the total area, accounting for areas above and below the x-axis. In this context, A(x) and F(x) are defined as definite integrals of the function ƒ(t) over specified intervals.
Recommended video:

Definition of the Definite Integral
Area Function
An area function, such as A(x) or F(x), is a function that gives the accumulated area under a curve from a specific starting point to a variable endpoint x. It is defined as the integral of a function from a constant lower limit to x, allowing for the evaluation of how the area changes as x varies. This concept is crucial for understanding how to compute areas based on the graph provided.
Recommended video:
Finding Area When Bounds Are Not Given
Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus links the concept of differentiation and integration, stating that if F is an antiderivative of f on an interval, then the integral of f from a to b is equal to F(b) - F(a). This theorem is essential for evaluating area functions, as it allows us to compute the definite integral by finding the antiderivative of the function and applying the limits of integration.
Recommended video:

Fundamental Theorem of Calculus Part 1

 5:23m
5:23mWatch next
Master Finding Area Between Curves on a Given Interval with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
44
views
