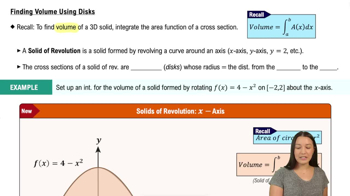
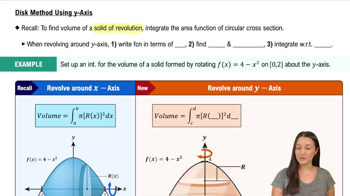
43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.
The region bounded by the curve y = 1+√x, the curve y = 1−√x, and the line x=1 is revolved about the y-axis. Find the volume of the resulting solid by (a) integrating with respect to x and (b) integrating with respect to y. Be sure your answers agree.