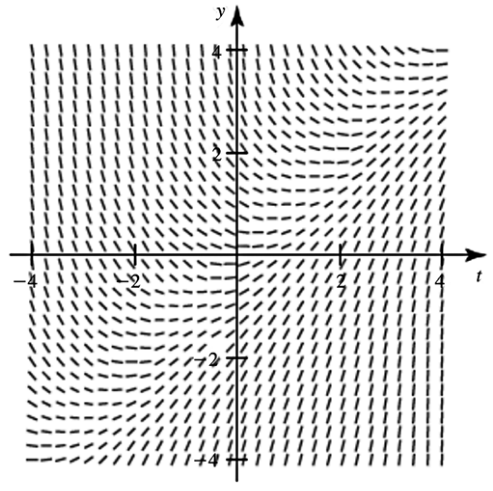
A second-order equation Consider the differential equation y''(t) - k²y(t) = 0 where k > 0 is a real number.
d. For a positive real number k, verify that the general solution of the equation may also be expressed in the form y(t) = C₁cosh(kt) + C₂sinh(kt), where cosh and sinh are the hyperbolic cosine and hyperbolic sine, respectively (Section 7.3).