Find two different explicit formulas for the sequence {1, -2, 3, -4, -5 .....}
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
14. Sequences & Series
Sequences
Problem 10.1.31c
Textbook Question
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
c. Find an explicit formula for the nth term of the sequence.
{1, 3, 9, 27, 81, ......}
 Verified step by step guidance
Verified step by step guidance1
Identify the pattern in the given sequence: {1, 3, 9, 27, 81, ...}. Notice how each term relates to the previous one by multiplication.
Recognize that the sequence is geometric because each term is obtained by multiplying the previous term by a constant ratio. Calculate the common ratio \( r \) by dividing the second term by the first term: \( r = \frac{3}{1} \).
Recall the general formula for the nth term of a geometric sequence: \( a_n = a_1 \times r^{n-1} \), where \( a_1 \) is the first term and \( r \) is the common ratio.
Substitute the known values into the formula: \( a_1 = 1 \) and \( r = 3 \), so the explicit formula becomes \( a_n = 1 \times 3^{n-1} \).
Simplify the formula if possible. In this case, the explicit formula for the nth term is \( a_n = 3^{n-1} \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sequences and Terms
A sequence is an ordered list of numbers where each number is called a term. The nth term, denoted as aₙ, represents the value at position n in the sequence. Understanding how terms progress helps in identifying patterns and formulating explicit expressions.
Recommended video:
Guided course
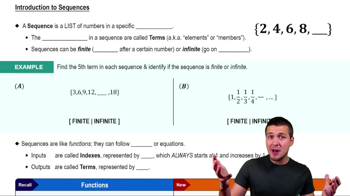
Introduction to Sequences
Geometric Sequences
A geometric sequence is one where each term is found by multiplying the previous term by a constant ratio. For example, in the sequence {1, 3, 9, 27, 81, ...}, each term is multiplied by 3. Recognizing this pattern is key to finding the explicit formula.
Recommended video:
Guided course
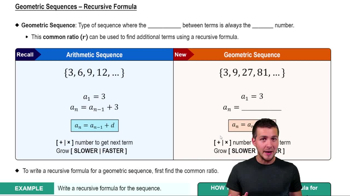
Geometric Sequences - Recursive Formula
Explicit Formula for nth Term
The explicit formula expresses the nth term directly in terms of n, without needing previous terms. For geometric sequences, it is generally aₙ = a₁ * r^(n-1), where a₁ is the first term and r is the common ratio. This formula allows quick calculation of any term.
Recommended video:

Divergence Test (nth Term Test)

 8:22m
8:22mWatch next
Master Introduction to Sequences with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
26
views
