Using the graph, find the specified limit or state that the limit does not exist (DNE). lim ⁡ x → − 2 − f ( x ) \lim_{x\rarr-2^{-}}f\left(x\right) lim x → − 2 − f ( x ) , lim ⁡ x → − 2 + f ( x ) \lim_{x\rarr-2^{+}}f\left(x\right) lim x → − 2 + f ( x ) , lim ⁡ x → − 2 f ( x ) \lim_{x\rarr-2^{}}f\left(x\right) lim x → − 2 f ( x )

lim ⁡ x → − 2 − − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = 1 \lim_{x\to-2^{-}}-f(x)=1,\lim_{x\to-2^{+}}f(x)=1,\lim_{x\to-2}f(x)=1

lim ⁡ x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = − 1 , lim ⁡ x → − 2 f ( x ) = D N E \lim_{x\to-2^{-}}f\left(x\right)=1,\lim_{x\to-2^{+}}f\left(x\right)=-1,\lim_{x\to-2}f\left(x\right)=DNE

lim ⁡ x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = D N E \lim_{x\to-2^{-}}f\left(x\right)=1,\lim_{x\to-2^{+}}f\left(x\right)=1,\lim_{x\to-2}f\left(x\right)=DNE

lim ⁡ x → − 2 − f ( x ) = 0 , lim ⁡ x → − 2 + f ( x ) = 0 , lim ⁡ x → − 2 f ( x ) = 0 \lim_{x\to-2^{-}}f\left(x\right)=0,\lim_{x\to-2^{+}}f\left(x\right)=0,\lim_{x\to-2}f\left(x\right)=0

Using the graph, find the specified limit or state that the limit does not exist (DNE). lim ⁡ x → 0 − f ( x ) \lim_{x\rightarrow0^{-}}f\left(x\right) lim x → 0 − f ( x ) , lim ⁡ x → 0 + f ( x ) \lim_{x\rightarrow0^{+}}f\left(x\right) lim x → 0 + f ( x ) , lim ⁡ x → 0 f ( x ) \lim_{x\rightarrow0}f\left(x\right) lim x → 0 f ( x )

lim ⁡ x → 0 − f ( x ) = 0 \lim_{x\rightarrow0^{-}}f\left(x\right)=0 lim x → 0 − f ( x ) = 0 , lim ⁡ x → 0 + f ( x ) = 0 \lim_{x\rightarrow0^{+}}f\left(x\right)=0 lim x → 0 + f ( x ) = 0 , lim ⁡ x → 0 f ( x ) = 0 \lim_{x\rightarrow0}f\left(x\right)=0 lim x → 0 f ( x ) = 0

lim ⁡ x → 0 − f ( x ) = 0 \lim_{x\rightarrow0^{-}}f\left(x\right)=0 lim x → 0 − f ( x ) = 0 , lim ⁡ x → 0 + f ( x ) = 0 \lim_{x\rightarrow0^{+}}f\left(x\right)=0 lim x → 0 + f ( x ) = 0 , lim ⁡ x → 0 f ( x ) = D N E \lim_{x\rightarrow0}f\left(x\right)=DNE lim x → 0 f ( x ) = D NE

lim ⁡ x → 0 − f ( x ) = − 1 \lim_{x\rightarrow0^{-}}f\left(x\right)=-1 lim x → 0 − f ( x ) = − 1 , lim ⁡ x → 0 + f ( x ) = − 1 \lim_{x\rightarrow0^{+}}f\left(x\right)=-1 lim x → 0 + f ( x ) = − 1 , lim ⁡ x → 0 f ( x ) = D N E \lim_{x\rightarrow0}f\left(x\right)=DNE lim x → 0 f ( x ) = D NE

lim ⁡ x → 0 − f ( x ) = − 1 \lim_{x\rightarrow0^{-}}f\left(x\right)=-1 lim x → 0 − f ( x ) = − 1 , lim ⁡ x → 0 + f ( x ) = − 1 \lim_{x\rightarrow0^{+}}f\left(x\right)=-1 lim x → 0 + f ( x ) = − 1 , lim ⁡ x → 0 f ( x ) = − 1 \lim_{x\rightarrow0}f\left(x\right)=-1 lim x → 0 f ( x ) = − 1

Using the graph, find the specified limit or state that the limit does not exist. lim ⁡ x → 4 − f ( x ) \lim_{x\rightarrow4^{-}}f\left(x\right) lim x → 4 − f ( x ) , lim ⁡ x → 4 + f ( x ) \lim_{x\rightarrow4^{+}}f\left(x\right) lim x → 4 + f ( x ) , lim ⁡ x → 4 f ( x ) \lim_{x\rightarrow4}f\left(x\right) lim x → 4 f ( x )

lim ⁡ x → 4 − f ( x ) = 1 \lim_{x\rightarrow4^{-}}f\left(x\right)=1 lim x → 4 − f ( x ) = 1 , lim ⁡ x → 4 + f ( x ) = 3 \lim_{x\rightarrow4^{+}}f\left(x\right)=3 lim x → 4 + f ( x ) = 3 , lim ⁡ x → 4 f ( x ) = D N E \lim_{x\rightarrow4}f\left(x\right)=DNE lim x → 4 f ( x ) = D NE

lim ⁡ x → 4 − f ( x ) = 1 \lim_{x\rightarrow4^{-}}f\left(x\right)=1 lim x → 4 − f ( x ) = 1 , lim ⁡ x → 4 + f ( x ) = 1 \lim_{x\rightarrow4^{+}}f\left(x\right)=1 lim x → 4 + f ( x ) = 1 , lim ⁡ x → 4 f ( x ) = 1 \lim_{x\rightarrow4}f\left(x\right)=1 lim x → 4 f ( x ) = 1

lim ⁡ x → 4 − f ( x ) = 3 \lim_{x\rightarrow4^{-}}f\left(x\right)=3 lim x → 4 − f ( x ) = 3 , lim ⁡ x → 4 + f ( x ) = 3 \lim_{x\rightarrow4^{+}}f\left(x\right)=3 lim x → 4 + f ( x ) = 3 , lim ⁡ x → 4 f ( x ) = 3 \lim_{x\rightarrow4}f\left(x\right)=3 lim x → 4 f ( x ) = 3

lim ⁡ x → 4 − f ( x ) = 3 \lim_{x\rightarrow4^{-}}f\left(x\right)=3 lim x → 4 − f ( x ) = 3 , lim ⁡ x → 4 + f ( x ) = 1 \lim_{x\rightarrow4^{+}}f\left(x\right)=1 lim x → 4 + f ( x ) = 1 , lim ⁡ x → 4 f ( x ) = D N E \lim_{x\rightarrow4}f\left(x\right)=DNE lim x → 4 f ( x ) = D NE

Find the specified limit or state that the limit does not exist by creating a table of values. f ( x ) = 1 x f\left(x\right)=\frac{1}{x} f ( x ) = x 1 lim ⁡ x → 1 − f ( x ) \lim_{x\rightarrow1^{-}}f\left(x\right) lim x → 1 − f ( x ) , lim ⁡ x → 1 + f ( x ) \lim_{x\rightarrow1^{+}}f\left(x\right) lim x → 1 + f ( x ) , lim ⁡ x → 1 f ( x ) \lim_{x\rightarrow1}f\left(x\right) lim x → 1 f ( x )

lim ⁡ x → 1 − f ( x ) = 1 \lim_{x\rightarrow1^{-}}f\left(x\right)=1 lim x → 1 − f ( x ) = 1 , lim ⁡ x → 1 + f ( x ) = 1 \lim_{x\rightarrow1^{+}}f\left(x\right)=1 lim x → 1 + f ( x ) = 1 , lim ⁡ x → 1 f ( x ) = 1 \lim_{x\rightarrow1}f\left(x\right)=1 lim x → 1 f ( x ) = 1

lim ⁡ x → 1 − f ( x ) = 0 \lim_{x\rightarrow1^{-}}f\left(x\right)=0 lim x → 1 − f ( x ) = 0 , lim ⁡ x → 1 + f ( x ) = 0 \lim_{x\rightarrow1^{+}}f\left(x\right)=0 lim x → 1 + f ( x ) = 0 , lim ⁡ x → 1 f ( x ) = 1 \lim_{x\rightarrow1}f\left(x\right)=1 lim x → 1 f ( x ) = 1

lim ⁡ x → 1 − f ( x ) = 1 \lim_{x\rightarrow1^{-}}f\left(x\right)=1 lim x → 1 − f ( x ) = 1 , lim ⁡ x → 1 + f ( x ) = − 1 \lim_{x\rightarrow1^{+}}f\left(x\right)=-1 lim x → 1 + f ( x ) = − 1 , lim ⁡ x → 1 f ( x ) = D N E \lim_{x\rightarrow1}f\left(x\right)=DNE lim x → 1 f ( x ) = D NE

lim ⁡ x → 1 − f ( x ) = − 1 \lim_{x\rightarrow1^{-}}f\left(x\right)=-1 lim x → 1 − f ( x ) = − 1 , lim ⁡ x → 1 + f ( x ) = − 1 \lim_{x\rightarrow1^{+}}f\left(x\right)=-1 lim x → 1 + f ( x ) = − 1 , lim ⁡ x → 1 f ( x ) = − 1 \lim_{x\rightarrow1}f\left(x\right)=-1 lim x → 1 f ( x ) = − 1

1. Limits and Continuity

Introduction to Limits

1. Limits and Continuity

Introduction to Limits: Videos & Practice Problems

Video Lessons Practice Worksheet

Topic summary

Limits are fundamental in calculus, representing the y-value a function approaches as x nears a specific value from either side. This can be analyzed graphically or numerically. One-sided limits, denoted with negative or positive signs, help determine behavior from the left or right. If the limits from both sides differ, the overall limit does not exist (DNE). Additionally, limits may not exist due to unbounded behavior (approaching infinity) or oscillation near a point. Understanding these concepts is crucial for analyzing functions and their continuity.

concept

Finding Limits Numerically and Graphically

Video duration:

Finding Limits Numerically and Graphically Video Summary

Limits are fundamental concepts in calculus that help us understand the behavior of functions as they approach a specific value. When we talk about limits, we are interested in what a function is doing around a certain value of x, rather than at that exact point. This can be visualized through graphs or analyzed using tables of values.

The notation for limits is typically expressed as $\lim_{{x \to c}} f(x)$, which reads as "the limit of $f(x)$ as $x$ approaches $c$." For example, to find the limit of the function $f(x) = x^2$ as $x$ approaches 2, we examine the y-values that $f(x)$ approaches as $x$ gets very close to 2. This means we consider values like 1.99 and 2.01, which yield results of 3.96 and 4.04, respectively. Both sides approach a y-value of 4, leading us to conclude that $\lim_{{x \to 2}} x^2 = 4$.

Another example involves the function $f(x) = x + 4$ as $x$ approaches 1. By evaluating values like 0.99 and 1.01, we find that both sides approach a y-value of 5. Thus, $\lim_{{x \to 1}} (x + 4) = 5$. It's important to note that while plugging in the value of $c$ directly into the function can yield the limit, this is not always reliable. There are cases where the limit does not equal the function value at that point.

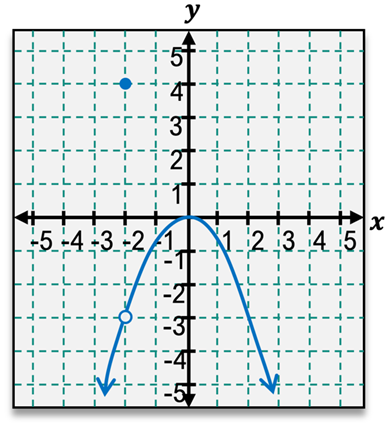
For instance, when examining a different function as $x$ approaches 3, we may find that the limit is 1, even if the function value at $x = 3$ is 4. This discrepancy highlights the importance of focusing on the behavior of the function around the point rather than the value at the point itself. Therefore, understanding limits requires careful analysis of the function's approach to a given value, ensuring we consider the surrounding values rather than just the point in question.

In summary, limits provide a way to analyze the behavior of functions as they approach specific values, using both graphical and numerical methods. This foundational concept is crucial for further studies in calculus and mathematical analysis.

Problem

Find the limit by creating a table of values.
$\lim_{x\rarr0}-4x+2$

$-4$

$-2$

$0$

$2$

Problem

Find the limit by creating a table of values.
$\lim_{x\rarr2}3x^2+5x+1$

$1$

$10$

$23$

$21$

Problem

Find the limit by creating a table of values.
$\lim_{x\rarr1}\frac{x^2-4}{x-2}$

$0$

$3$

$-3$

$2$

Problem

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr1}f\left(x\right)$

$2$

$1$

$0$

Unable to determine

Problem

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr-2}f\left(x\right)$

$4$

$-2$

$-3$

Unable to determine

Problem

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr4}f\left(x\right)$

$2$

$-2$

$0$

Unable to determine

example

Finding Limits Numerically and Graphically Example 1

Video duration:

Finding Limits Numerically and Graphically Example 1 Video Summary

In analyzing limits using a graph, it's essential to observe the behavior of the function as the input approaches a specific value from both the left and right sides. This approach helps in estimating the limit accurately, even when the function may not be defined at that point.

For instance, to find the limit of $ f(x) $ as $ x $ approaches $-2$, we examine the graph near $-2$. As $ x $ approaches $-2$ from the left, the function approaches a value of $ 1 $. Similarly, approaching from the right also leads to a value of $ 1 $. Therefore, we conclude that:

\[ \lim_{{x \to -2}} f(x) = 1 \]

Next, we consider the limit of $ f(x) $ as $ x $ approaches $ 0 $. Observing the graph, as $ x $ approaches $ 0 $ from both sides, the function approaches $ 0 $. Despite a hole in the graph at $ x = 0 $, the limit is determined by the values the function approaches, not the value at $ 0 $. Thus, we find:

\[ \lim_{{x \to 0}} f(x) = 0 \]

Finally, for the limit of $ f(x) $ as $ x $ approaches $ 3 $, we again look at the graph. From both the left and right sides, the function approaches $ 1 $. Therefore, we conclude:

\[ \lim_{{x \to 3}} f(x) = 1 \]

It's important to note that limits can behave differently depending on the direction of approach. For example, if we were to analyze the limit as $ x $ approaches $ 4 $, we might observe that the function approaches $ 1 $ from one side but not from the other. This discrepancy indicates that the limit does not exist at that point, highlighting the importance of considering both sides when determining limits.

concept

One-Sided Limits

Video duration:

One-Sided Limits Video Summary

When determining the limit of a function as the variable approaches a specific value, we focus on the y-value that the function approaches as x gets very close to that value from either side. This process involves evaluating one-sided limits, which are expressed using specific notation. For a left-sided limit, we denote it as $\lim_{{x \to c^-}} f(x)$, indicating that x approaches c from the left. Conversely, a right-sided limit is denoted as $\lim_{{x \to c^+}} f(x)$, indicating that x approaches c from the right. The negative sign indicates the left side, while the positive sign indicates the right side, which can be remembered by considering the coordinate system where x-values to the left are negative and those to the right are positive.

To illustrate this, consider a piecewise function. For example, to find the left-sided limit as x approaches 3, we evaluate $\lim_{{x \to 3^-}} f(x)$. By examining the graph or substituting values close to 3 from the left (like 2.99 and 2.999), we find that the function approaches a y-value of 1. Thus, the left-sided limit is 1. For the right-sided limit, $\lim_{{x \to 3^+}} f(x)$, we find that as x approaches 3 from the right (using values like 3.01 and 3.001), the function approaches a y-value of 4. Therefore, the right-sided limit is 4.

When we consider the overall limit as x approaches 3, $\lim_{{x \to 3}} f(x)$, we notice that the left-sided limit (1) and the right-sided limit (4) are not equal. This discrepancy indicates that the limit does not exist, often abbreviated as DNE (Does Not Exist).

In another example, if we evaluate the limit as x approaches 1, we find the left-sided limit $\lim_{{x \to 1^-}} f(x)$ is -1, and the right-sided limit $\lim_{{x \to 1^+}} f(x)$ is also -1. Since both one-sided limits are equal, we conclude that the overall limit as x approaches 1 is -1.

In summary, when working with one-sided limits, if the left-sided and right-sided limits are not equal, the overall limit does not exist. However, if they are equal, the overall limit exists and is equal to that common value. This understanding is crucial for analyzing the behavior of functions at specific points.

Problem

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rarr-2^{-}}f\left(x\right)$ , $\lim_{x\rarr-2^{+}}f\left(x\right)$ , $\lim_{x\rarr-2^{}}f\left(x\right)$

$\lim_{x \to - 2^{-}} - f (x) = 1, \lim_{x \to - 2^{+}} f (x) = 1, \lim_{x \to - 2} f (x) = 1$

$\lim_{x \to - 2^{-}} f (x) = 1, \lim_{x \to - 2^{+}} f (x) = - 1, \lim_{x \to - 2} f (x) = D N E$

$\lim_{x \to - 2^{-}} f (x) = 1, \lim_{x \to - 2^{+}} f (x) = 1, \lim_{x \to - 2} f (x) = D N E$

$\lim_{x \to - 2^{-}} f (x) = 0, \lim_{x \to - 2^{+}} f (x) = 0, \lim_{x \to - 2} f (x) = 0$

Problem

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rightarrow0^{-}}f\left(x\right)$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)$ , $\lim_{x\rightarrow0}f\left(x\right)$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=0$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=0$ , $\lim_{x\rightarrow0}f\left(x\right)=0$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=0$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=0$ , $\lim_{x\rightarrow0}f\left(x\right)=DNE$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0}f\left(x\right)=DNE$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0}f\left(x\right)=-1$

Problem

Using the graph, find the specified limit or state that the limit does not exist.
$\lim_{x\rightarrow4^{-}}f\left(x\right)$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)$ , $\lim_{x\rightarrow4}f\left(x\right)$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=1$ , $\lim_{x\rightarrow4}f\left(x\right)=1$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=3$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=3$ , $\lim_{x\rightarrow4}f\left(x\right)=3$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=3$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=1$ , $\lim_{x\rightarrow4}f\left(x\right)=DNE$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=3$ , $\lim_{x\rightarrow4}f\left(x\right)=DNE$

Problem

Find the specified limit or state that the limit does not exist by creating a table of values.
$f\left(x\right)=\frac{1}{x}$
$\lim_{x\rightarrow1^{-}}f\left(x\right)$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)$ , $\lim_{x\rightarrow1}f\left(x\right)$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=0$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=0$ , $\lim_{x\rightarrow1}f\left(x\right)=1$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=1$ , $\lim_{x\rightarrow1}f\left(x\right)=1$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow1}f\left(x\right)=DNE$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=-1$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow1}f\left(x\right)=-1$

concept

Cases Where Limits Do Not Exist

Video duration:

Cases Where Limits Do Not Exist Video Summary

Understanding when a limit does not exist is crucial in calculus, as it helps in analyzing the behavior of functions. There are several scenarios where limits fail to exist, and recognizing these can enhance your problem-solving skills.

One common case occurs with piecewise functions that exhibit a jump discontinuity. For instance, consider the limit of a function $ f(x) $ as $ x $ approaches 3. If the function approaches a value of 1 from the left and a value of 4 from the right, the limit does not exist because the left-hand limit and right-hand limit are not equal. This discontinuity is a clear indicator that the limit is undefined.

Another scenario involves unbounded behavior, often seen in rational functions with vertical asymptotes. For example, if we examine the limit of $ f(x) $ as $ x $ approaches 2 and find that the function approaches infinity from both sides, we conclude that the limit does not exist. This is because infinity is not a finite number, and thus, we cannot assign a limit value in this case. It’s important to note that while we may describe the behavior of the function as approaching positive or negative infinity, this does not imply the existence of a limit.

Lastly, oscillating functions present another challenge. For instance, if we look at the limit of $ f(x) $ as $ x $ approaches 0 and observe that the function oscillates wildly without settling on a particular value, the limit does not exist. This behavior is typical for functions like $ \sin\left(\frac{1}{x}\right) $ or $ \cos\left(\frac{1}{x}\right) $, where zooming in on the graph only reveals more oscillation rather than convergence to a specific value.

In summary, limits do not exist in cases of jump discontinuities, unbounded behavior, and oscillation. Recognizing these patterns will aid in your understanding of limits and their applications in calculus.

example

Cases Where Limits Do Not Exist Example 2

Video duration:

Cases Where Limits Do Not Exist Example 2 Video Summary

Understanding limits is crucial in calculus, particularly when analyzing the behavior of functions as they approach specific values. In this context, we will explore how to estimate limits using graphical representations and identify when limits do not exist.

To begin, consider the limit of $ f(x) $ as $ x $ approaches $-2$. By examining the graph, we observe that as $ x $ approaches $-2$ from both the left and the right, the function approaches a value of $ 0 $. Therefore, we conclude that:

\[ \lim_{{x \to -2}} f(x) = 0 \]

It is important to note that the behavior of the function at values other than $-2$ (such as $-3$) does not affect the limit at $-2$. Limits focus solely on the values of the function as $ x $ gets infinitely close to the specified point.

Next, we analyze the limit of $ f(x) $ as $ x $ approaches $ 0 $. Observing the graph again, we find that as $ x $ approaches $ 0 $ from both sides, the function approaches $ 1 $. Thus, we can state:

\[ \lim_{{x \to 0}} f(x) = 1 \]

Even though there is a hole in the graph at $ x = 0 $ where the function value is actually $-2$, this does not impact the limit since we are concerned with the behavior of the function as it approaches $ 0 $, not the value at $ 0 $.

Finally, we examine the limit of $ f(x) $ as $ x $ approaches $-3$. The graph indicates that as $ x $ approaches $-3$ from the left, the function approaches $ 1 $. However, from the right, the function exhibits unbounded behavior, tending towards negative infinity. This discrepancy between the left-hand limit and the right-hand limit leads us to conclude that:

\[ \lim_{{x \to -3}} f(x) \text{ does not exist} \]

Since the one-sided limits are not equal, and one of them is unbounded, the overall limit at this point is undefined. Understanding these concepts is essential for mastering limits and their implications in calculus.

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr1}f\left(x\right)$

$0$

$1$

$2$

$DNE$

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr-2}f\left(x\right)$

$-3$

$1$

$4$

$D N E$

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr0}f\left(x\right)$

$0$

$1$

$5$

$DNE$

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr0}f\left(x\right)$

$-1$

$0$

$1$

$DNE$

Do you want more practice?

More sets

Introduction to Limits

1. Limits and Continuity

5 problems

Topic

1. Limits and Continuity

3 topics 7 problems

Chapter

Go over this topic definitions with flashcards

More sets

Introduction to Limits quiz #1
1. Limits and Continuity
16 Terms

Here’s what students ask on this topic:

What is the definition of a limit in calculus?

A limit in calculus is the value that a function (f(x)) approaches as the input (x) approaches a certain value (c). It is denoted as lim_x→c f(x). The limit helps in understanding the behavior of functions at specific points, especially where the function may not be explicitly defined. Limits can be evaluated graphically by observing the function's behavior near the point or numerically by creating a table of values approaching the point from both sides.

How do you find the limit of a function using a graph?

To find the limit of a function using a graph, observe the y-values that the function approaches as x gets close to the target value from both the left and right sides. If the y-values from both sides converge to the same value, that value is the limit. For example, if the graph of f(x) shows that as x approaches 2 from both sides, the y-value approaches 4, then the limit of f(x) as x approaches 2 is 4.

What are one-sided limits and how are they different from regular limits?

One-sided limits consider the behavior of a function as x approaches a specific value from only one side—either the left or the right. They are denoted as lim_x→c^- f(x) for the left-sided limit and lim_x→c⁺ f(x) for the right-sided limit. Regular limits, denoted as lim_x→c f(x), require the function to approach the same value from both sides. If the one-sided limits are not equal, the regular limit does not exist (DNE).

When does a limit not exist?

A limit does not exist in several scenarios: (1) When the function approaches different values from the left and right sides of the target value. (2) When the function exhibits unbounded behavior, meaning it goes to infinity or negative infinity as x approaches the target value. (3) When the function oscillates near the target value, such as with functions like sin(1/x) or cos(1/x). In these cases, the limit is said to be DNE (does not exist).

How do you find the limit of a piecewise function?

To find the limit of a piecewise function, evaluate the limit from both the left and right sides of the target value using the appropriate piece of the function. If the function approaches the same value from both sides, that value is the limit. If the values differ, the limit does not exist. For example, if f(x) = {x-2 for x<3, 4 for x≥3}, the limit as x approaches 3 from the left is 1, and from the right is 4, so the overall limit does not exist.

Your Calculus tutors

Additional resources for Introduction to Limits

PRACTICE PROBLEMS AND ACTIVITIES (277)

Introduction to Limits: Videos & Practice Problems

Finding Limits Numerically and Graphically

Finding Limits Numerically and Graphically Video Summary

Find the limit by creating a table of values.limx→0−4x+2\lim_{x\rarr0}-4x+2limx→0−4x+2

Find the limit by creating a table of values.limx→23x2+5x+1\lim_{x\rarr2}3x^2+5x+1limx→23x2+5x+1

Find the limit by creating a table of values.limx→1x2−4x−2\lim_{x\rarr1}\frac{x^2-4}{x-2}limx→1x−2x2−4

Find the limit using the graph of f(x)f\left(x\right)f(x)shown.limx→1f(x)\lim_{x\rarr1}f\left(x\right)limx→1f(x)

Find the limit using the graph of f(x)f\left(x\right)f(x)shown.limx→−2f(x)\lim_{x\rarr-2}f\left(x\right)limx→−2f(x)

Find the limit using the graph of f(x)f\left(x\right)f(x)shown.limx→4f(x)\lim_{x\rarr4}f\left(x\right)limx→4f(x)

Finding Limits Numerically and Graphically Example 1

Finding Limits Numerically and Graphically Example 1 Video Summary

One-Sided Limits

One-Sided Limits Video Summary

Using the graph, find the specified limit or state that the limit does not exist (DNE).limx→−2−f(x)\lim_{x\rarr-2^{-}}f\left(x\right)limx→−2−f(x), limx→−2+f(x)\lim_{x\rarr-2^{+}}f\left(x\right)limx→−2+f(x), limx→−2f(x)\lim_{x\rarr-2^{}}f\left(x\right)limx→−2f(x)

Using the graph, find the specified limit or state that the limit does not exist (DNE).limx→0−f(x)\lim_{x\rightarrow0^{-}}f\left(x\right)limx→0−f(x) , limx→0+f(x)\lim_{x\rightarrow0^{+}}f\left(x\right)limx→0+f(x), limx→0f(x)\lim_{x\rightarrow0}f\left(x\right)limx→0f(x)

Using the graph, find the specified limit or state that the limit does not exist.limx→4−f(x)\lim_{x\rightarrow4^{-}}f\left(x\right)limx→4−f(x), limx→4+f(x)\lim_{x\rightarrow4^{+}}f\left(x\right)limx→4+f(x), limx→4f(x)\lim_{x\rightarrow4}f\left(x\right)limx→4f(x)

Cases Where Limits Do Not Exist

Cases Where Limits Do Not Exist Video Summary

Cases Where Limits Do Not Exist Example 2

Cases Where Limits Do Not Exist Example 2 Video Summary

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→1f(x)\lim_{x\rarr1}f\left(x\right)limx→1f(x)

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→−2f(x)\lim_{x\rarr-2}f\left(x\right)limx→−2f(x)

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→0f(x)\lim_{x\rarr0}f\left(x\right)limx→0f(x)

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→0f(x)\lim_{x\rarr0}f\left(x\right)limx→0f(x)

Do you want more practice?

Go over this topic definitions with flashcards

Here’s what students ask on this topic:

What is the definition of a limit in calculus?

How do you find the limit of a function using a graph?

What are one-sided limits and how are they different from regular limits?

When does a limit not exist?

How do you find the limit of a piecewise function?

Your Calculus tutors

Find the limit by creating a table of values.
$\lim_{x\rarr0}-4x+2$

Find the limit by creating a table of values.
$\lim_{x\rarr2}3x^2+5x+1$

Find the limit by creating a table of values.
$\lim_{x\rarr1}\frac{x^2-4}{x-2}$

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr1}f\left(x\right)$

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr-2}f\left(x\right)$

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr4}f\left(x\right)$

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rarr-2^{-}}f\left(x\right)$ , $\lim_{x\rarr-2^{+}}f\left(x\right)$ , $\lim_{x\rarr-2^{}}f\left(x\right)$

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rightarrow0^{-}}f\left(x\right)$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)$ , $\lim_{x\rightarrow0}f\left(x\right)$

Using the graph, find the specified limit or state that the limit does not exist.
$\lim_{x\rightarrow4^{-}}f\left(x\right)$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)$ , $\lim_{x\rightarrow4}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr1}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr-2}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr0}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr0}f\left(x\right)$