For what values of p does the series ∑ (k = 10 to ∞) 1 / kᵖ converge (initial index is 10)? For what values of p does it diverge?
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
14. Sequences & Series
Convergence Tests
Problem 10.6.49
Textbook Question
45–63. Absolute and conditional convergence Determine whether the following series converge absolutely, converge conditionally, or diverge.
∑ (k = 1 to ∞) (3/4)ᵏ
 Verified step by step guidance
Verified step by step guidance1
Identify the given series: \( \sum_{k=1}^{\infty} \left( \frac{3}{4} \right)^k \). This is a geometric series with common ratio \( r = \frac{3}{4} \).
Recall that a geometric series \( \sum_{k=1}^{\infty} ar^{k} \) converges if and only if \( |r| < 1 \). Since \( \left| \frac{3}{4} \right| = 0.75 < 1 \), the series converges.
Because the terms \( \left( \frac{3}{4} \right)^k \) are positive, the series is absolutely convergent. Absolute convergence means the series of absolute values \( \sum |a_k| \) converges, which is true here since all terms are positive.
To confirm, write the sum of the geometric series using the formula for \( |r| < 1 \): \[ S = \frac{a}{1 - r} \], where \( a = \left( \frac{3}{4} \right)^1 = \frac{3}{4} \).
Summarize: Since the series converges absolutely, it also converges conditionally by default, but the stronger conclusion is absolute convergence.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Absolute Convergence
A series ∑a_k converges absolutely if the series of absolute values ∑|a_k| converges. Absolute convergence guarantees convergence regardless of the sign of terms, and it implies the original series converges. This concept helps distinguish between strong convergence and conditional cases.
Recommended video:
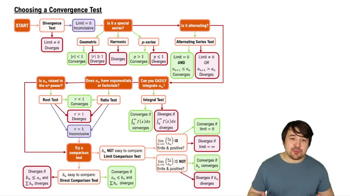
Choosing a Convergence Test
Geometric Series and Its Convergence
A geometric series has the form ∑r^k, where r is a constant ratio. It converges if and only if |r| < 1, and its sum is given by a/(1-r) for the first term a. Recognizing a series as geometric simplifies determining convergence and sum.
Recommended video:

Geometric Series
Conditional Convergence
A series converges conditionally if it converges but does not converge absolutely. This means the series ∑a_k converges, but ∑|a_k| diverges. Conditional convergence often occurs in alternating series and requires careful analysis beyond absolute value tests.
Recommended video:

Choosing a Convergence Test

 5:44m
5:44mWatch next
Master Divergence Test (nth Term Test) with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
23
views
