Solve the differential equation by separation of variables.
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
13. Intro to Differential Equations
Basics of Differential Equations
Problem 9.5.1
Textbook Question
Explain how the growth rate function determines the solution of a population model.
 Verified step by step guidance
Verified step by step guidance1
Understand that in population models, the growth rate function describes how the population changes over time, often expressed as a function of the current population size, say \(r(P)\), where \(P\) is the population at time \(t\).
Recognize that the population model is typically formulated as a differential equation of the form \(\frac{dP}{dt} = r(P) \cdot P\), where \(\frac{dP}{dt}\) represents the rate of change of the population with respect to time.
Analyze how the form of the growth rate function \(r(P)\) influences the behavior of the solution: for example, if \(r(P)\) is constant and positive, the population grows exponentially; if \(r(P)\) decreases as \(P\) increases, it may model limited resources leading to logistic growth.
Solve the differential equation by separating variables or using an integrating factor, depending on the form of \(r(P)\), to find the explicit solution \(P(t)\) that describes the population at any time \(t\).
Interpret the solution \(P(t)\) in terms of the growth rate function to understand long-term behavior such as equilibrium points, carrying capacity, or unbounded growth, which are all determined by the characteristics of \(r(P)\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Growth Rate Function
The growth rate function describes how the population changes over time, often expressed as a rate of change dependent on the current population size. It can be constant or vary with population, influencing whether the population grows, declines, or stabilizes.
Recommended video:
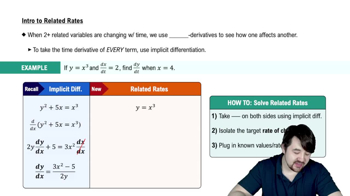
Intro To Related Rates
Differential Equations in Population Models
Population models are typically formulated as differential equations where the growth rate function defines the derivative of the population with respect to time. Solving these equations provides the population size as a function of time, revealing the dynamics of growth.
Recommended video:

Classifying Differential Equations
Equilibrium Solutions and Stability
Equilibrium solutions occur when the growth rate is zero, indicating a stable or unstable population size. Analyzing these points helps predict long-term behavior of the population, such as whether it will settle at a steady state or experience unbounded growth or decline.
Recommended video:
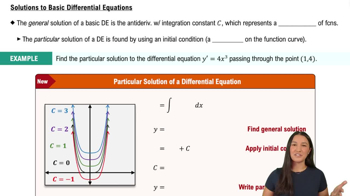
Solutions to Basic Differential Equations
Related Videos
Related Practice
Multiple Choice
93
views


