Differentiability: Videos & Practice Problems

Continuity and differentiability are crucial concepts in calculus. A function is continuous if it has no holes, jumps, or asymptotes, allowing for a smooth sketch without lifting the pencil. Differentiability requires continuity and a smooth graph without sharp corners. For piecewise functions, check continuity by ensuring the left and right limits at a point are equal. If the derivatives from both sides at that point are also equal, the function is differentiable. Otherwise, it may be continuous but not differentiable, highlighting the relationship between these two concepts.

Determining Differentiability Graphically

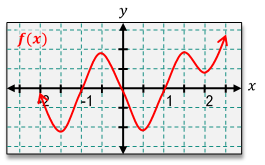
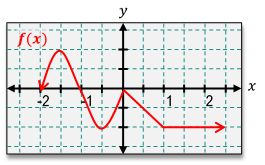
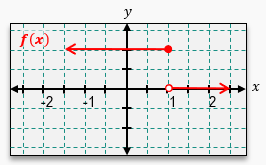
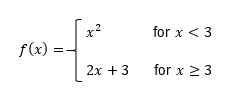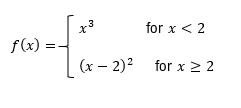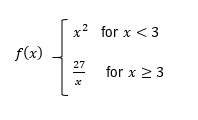Understanding the concepts of continuity and differentiability is essential in calculus. A function is considered continuous if its graph can be drawn without lifting the pencil, meaning there are no holes, jumps, or asymptotes. For a function to be differentiable, the derivative must exist at all points, which implies that the function must be continuous and smooth, without any sharp corners or turns.

To determine if a function is continuous at a specific point, such as x = 2, we check if the limit from both sides of that point equals the function's value at that point. If both the limit and the function value are equal, the function is continuous. For differentiability, we first confirm continuity and then examine the graph for any sharp corners. If a sharp corner exists, the function is not differentiable at that point, even if it is continuous.

For example, if we analyze a function at x = -3 and find a hole in the graph, we conclude that the function is not continuous, and consequently, it is not differentiable. Conversely, if we check x = 0 and find that the function is continuous but has a sharp corner, it is continuous but not differentiable. In another case, examining the interval from 0 to infinity, if the graph is smooth and continuous throughout, we can conclude that the function is both continuous and differentiable.

In summary, while a function can be continuous without being differentiable, it cannot be differentiable if it is not continuous. This relationship is crucial for solving problems related to the behavior of functions in calculus.

Determine if the graph of the function $f\left(x\right)$is continuous and/or differentiable at $x=2$.

• A. Continuous and non-differentiable
• B. Continuous and differentiable
• C. Discontinuous and non-differentiable
• D. Discontinuous and differentiable

Answer: (B)

Determine if the graph of the function $f\left(x\right)$is continuous and/or differentiable at $x=1$.

• A. Continuous and non-differentiable
• B. Continuous and differentiable
• C. Discontinuous and non-differentiable
• D. Discontinuous and differentiable

Answer: (A)

Determine if the graph of the function $f\left(x\right)$is continuous and/or differentiable at $x=1$.

• A. Continuous and non-differentiable
• B. Continuous and differentiable
• C. Discontinuous and non-differentiable
• D. Discontinuous and differentiable

Answer: (C)

Determining Differentiability Without A Graph

In the study of differentiability, a function is considered differentiable if it is both continuous and smooth. To determine differentiability without a graph, we can analyze the function algebraically, particularly when dealing with piecewise functions. A key aspect to remember is that polynomials are always differentiable. For instance, if we have a piecewise function composed of two polynomials, we can conclude that each polynomial is differentiable on its own.

However, the critical step is to examine the point where the two pieces meet, often referred to as the "value of interest." In this case, we can check the continuity of the function at this point by ensuring that the left-hand limit equals the right-hand limit. For example, if we evaluate the function at the value of interest, say \( x = 2 \), we can substitute this value into both pieces of the function. If both sides yield the same result, the function is continuous at that point.

To further assess differentiability, we need to check if the derivatives from both sides at the value of interest are equal. The derivative of a function can be found using the limit definition of the derivative, which is expressed as:

\[ f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} \]

For the left side, if the function is \( f(x) = x \), the derivative at \( x = 2 \) simplifies to 1. For the right side, if the function is \( f(x) = x^2 - 2 \), we would similarly apply the limit definition, leading to a derivative of \( 2x \). Evaluating this at \( x = 2 \) gives us 4.

In this scenario, since the left-hand derivative (1) does not equal the right-hand derivative (4), we conclude that while the function is continuous at \( x = 2 \), it is not differentiable there. Thus, the function is continuous but not differentiable at the point of interest.

This method of analyzing piecewise functions allows us to determine differentiability using algebraic techniques, reinforcing the importance of continuity and the behavior of derivatives at critical points.

Determine if the function$f\left(x\right)$ is continuous and/or differentiable at $x=3$.

• A. Continuous and non-differentiable
• B. Continuous and differentiable
• C. Discontinuous and non-differentiable
• D. Discontinuous and differentiable

Answer: (A)

Determine if the function$f\left(x\right)$ is continuous and/or differentiable at $x=2$.

• A. Continuous and non-differentiable
• B. Continuous and differentiable
• C. Discontinuous and non-differentiable
• D. Discontinuous and differentiable

Answer: (C)

Determine where the function $f\left(x\right)$ is not differentiable.
$f\left(x\right)=\frac{3}{x+2}$

• A. 0
• B. 2
• C. -2
• D. 3

Answer: (C)

Determine if the function$f\left(x\right)$ is continuous and/or differentiable at $x=3$.

• A. Continuous and non-differentiable
• B. Continuous and differentiable
• C. Discontinuous and non-differentiable
• D. Discontinuous and differentiable

Answer: (A)

Here’s what students ask on this topic:

What is the difference between continuity and differentiability in calculus?

Continuity and differentiability are fundamental concepts in calculus. A function is continuous if it has no holes, jumps, or asymptotes, meaning you can sketch the function without lifting your pencil. Mathematically, a function f(x) is continuous at a point x = c if the limit of f(x) as x approaches c from both sides equals f(c). Differentiability, on the other hand, requires the function to be continuous and smooth, without any sharp corners or cusps. A function is differentiable at a point if its derivative exists at that point. Therefore, all differentiable functions are continuous, but not all continuous functions are differentiable.

How do you determine if a function is differentiable at a point?

To determine if a function is differentiable at a point x = c, follow these steps: First, check if the function is continuous at x = c by ensuring the limit of the function from both sides equals the function's value at that point. Next, check for smoothness by ensuring there are no sharp corners or cusps at x = c. Mathematically, this involves checking if the left-hand derivative and the right-hand derivative at x = c are equal. If both conditions are met, the function is differentiable at that point.

Can a function be continuous but not differentiable? Provide an example.

Yes, a function can be continuous but not differentiable. A classic example is the absolute value function f(x) = |x|. This function is continuous everywhere, including at x = 0, but it is not differentiable at x = 0 because there is a sharp corner at that point. The left-hand derivative at x = 0 is -1, and the right-hand derivative is 1, so they are not equal, making the function non-differentiable at x = 0.

How do you check the differentiability of a piecewise function?

To check the differentiability of a piecewise function, follow these steps: First, ensure the function is continuous at the points where the pieces meet by checking if the left-hand limit equals the right-hand limit at those points. Next, find the derivatives of each piece and check if the left-hand derivative equals the right-hand derivative at the points of interest. If both conditions are satisfied, the piecewise function is differentiable at those points. Otherwise, it may be continuous but not differentiable.

What are the criteria for a function to be differentiable?

For a function to be differentiable at a point x = c, it must meet the following criteria: 1) The function must be continuous at x = c, meaning the limit of the function as x approaches c from both sides equals the function's value at that point. 2) The function must be smooth at x = c, meaning there are no sharp corners or cusps. Mathematically, this requires the left-hand derivative and the right-hand derivative at x = c to be equal. If both criteria are met, the function is differentiable at that point.