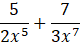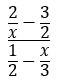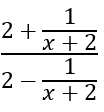Table of contents
- 0. Review of Algebra(0)
- 1. Equations & Inequalities(0)
- 2. Graphs of Equations(0)
- 3. Functions(0)
- 4. Polynomial Functions(0)
- 5. Rational Functions(0)
- 6. Exponential & Logarithmic Functions(0)
- 7. Systems of Equations & Matrices(0)
- 8. Conic Sections(0)
- 9. Sequences, Series, & Induction(0)
- 10. Combinatorics & Probability(0)
0. Review of Algebra
Algebraic Expressions
0. Review of Algebra
Algebraic Expressions: Videos & Practice Problems
Algebraic Expressions Practice Problems
44 problems