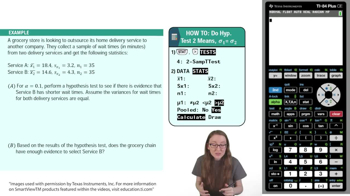
10. Hypothesis Testing for Two Samples

For ${\bar{x}}_1=41,S_{x1}=8.3,n_1=40,{\bar{x}}_2=39,S_{x2}=5.8$, & $n_2=50$, perform a hypothesis test to test the claim that ${\mu }_1>{\mu }_2$, assuming ${\sigma }_1={\sigma }_2$ for $\alpha =0.01$.

Find the critical value(s) for the alternative hypothesis, level of significance , and sample sizes and . Assume that the samples are random and independent, the populations are normally distributed, and the population variances are (a) equal .

Ha:μ1<μ2 , α=0.10 , n1=30 , n2=32

Test the claim about the difference between two population means and at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1<μ2, α=0.10, Assume (σ1)^2=(σ2)^2

Sample statistics:

x̅1=0.345, s1=0.305 , n1=11 and x̅2=0.515, s2=0.215, n2=9

Yellowfin Tuna

A marine biologist claims that the mean fork length (see figure at the left) of yellowfin tuna is different in two zones in the eastern tropical Pacific Ocean. A sample of 26 yellowfin tuna collected in Zone A has a mean fork length of 76.2 centimeters and a standard deviation of 16.5 centimeters. A sample of 31 yellowfin tuna collected in Zone B has a mean fork length of 80.8 centimeters and a standard deviation of 23.4 centimeters. At ,α=0.01 can you support the marine biologist’s claim? Assume the population variances are equal. (Adapted from Fishery Bulletin)

An education organization claims that the mean SAT scores for male athletes and male non-athletes at a college are different. A random sample of 26 male athletes at the college has a mean SAT score of 1189 and a standard deviation of 218. A random sample of 18 male non-athletes at the college has a mean SAT score of 1376 and a standard deviation of 186. At α=0.05, can you support the organization’s claim? Interpret the decision in the context of the original claim. Assume the populations are normally distributed and the population variances are equal.