10. Hypothesis Testing for Two Samples

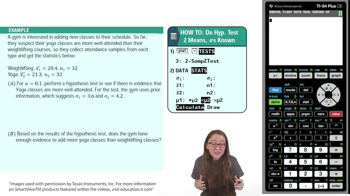
For ${\bar{x}}_1=40,{\sigma }_1=8.3,n_1=40,{\bar{x}}_2=39,{\sigma }_2=5.8$, & $n_2=50$, perform a hypothesis test to test the claim that ${\mu }_1>{\mu }_2$ for $\alpha =0.05$.

In Exercises 11–14, test the claim about the difference between two population means and at the level of significance . Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1=μ2; α=0.1

Population statistics:σ1=3.4 and σ2=1.5

Sample Statistics: x̅1=16, n1=29, x̅2=14, n2=28

In Exercises 11–14, test the claim about the difference between two population means and at the level of significance . Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1>μ2; α=0.10

Population statistics:σ1=40 and σ2=15

Sample Statistics: x̅1=500, n1=100, x̅2=495, n2=75

Testing the Difference Between Two Means In Exercises 15–24, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Bed-in-a-Box To compare customer satisfaction with mattresses that are delivered compressed in a box and traditional mattresses, a researcher randomly selects 30 ratings of mattresses in boxes and 30 ratings of traditional mattresses. The mean rating of mattresses in boxes is 68.7 out of 100. Assume the population standard deviation is 6.6. The mean rating of traditional mattresses is 70.9 out of 100. Assume the population standard deviation is 5.6. At α=0.01, can the researcher support the claim that the mean rating of traditional mattresses is greater than the mean rating of mattresses in a box? (Adapted from Consumer Reports)

Testing the Difference Between Two Means In Exercises 15–24, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

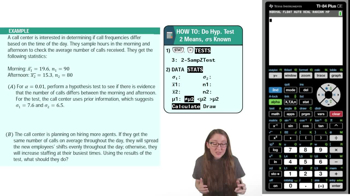
Repair Costs: Washing Machines You want to buy a washing machine, and a salesperson tells you that the mean repair costs for Model A and Model B are equal. You research the repair costs. The mean repair cost of 24 Model A washing machines is \$208. Assume the population standard deviation is \$18. The mean repair cost of 26 Model B washing machines is \$221. Assume the population standard deviation is \$22. At α=0.01, can you reject the salesperson’s claim?