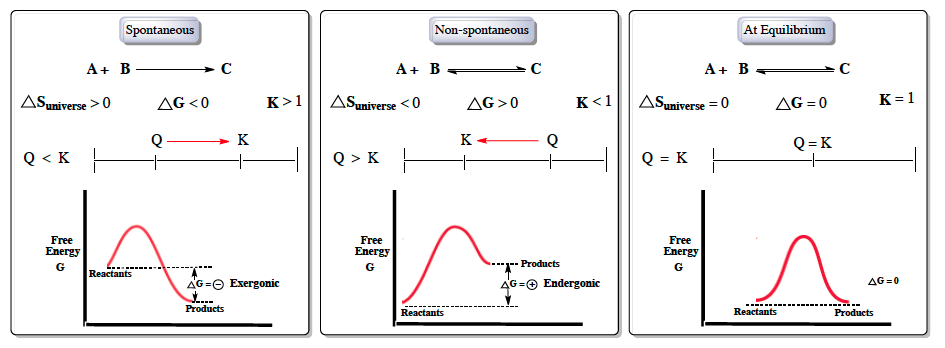
Gibbs free energy is a crucial concept in thermodynamics, particularly when discussing spontaneous reactions, which occur naturally without external energy input. In contrast, non-spontaneous reactions require energy to proceed. Understanding the relationship between Gibbs free energy, entropy, and equilibrium is essential for predicting the direction of chemical reactions.
For a reaction to be spontaneous, the entropy of the universe must be greater than zero, indicating an increase in disorder, in accordance with the second law of thermodynamics. The Gibbs free energy change (ΔG) must be less than zero, and the equilibrium constant (K) should be greater than one. This means that the reactants (A and B) naturally convert to products (C), and the reaction quotient (Q) must be less than K, indicating that the system will shift forward to reach equilibrium.
In energy diagrams, spontaneous reactions are represented by products having lower energy than reactants. The relationship can be expressed with the equation:
\[\Delta G = \text{Products} - \text{Reactants}\]
For spontaneous reactions, this results in a negative ΔG, indicating an exergonic process.
Conversely, non-spontaneous reactions exhibit the opposite characteristics: the entropy of the universe is less than zero, ΔG is greater than zero, and K is less than one. In this case, the reaction is not favorable in the forward direction but can proceed in reverse. Here, Q is greater than K, leading to a shift towards equilibrium in the reverse direction. The energy diagram for non-spontaneous reactions shows products at a higher energy level than reactants, resulting in a positive ΔG, which is termed endergonic.
At equilibrium, the system is balanced, with ΔS of the universe equal to zero, ΔG equal to zero, and K equal to one. The reaction quotient Q equals the equilibrium constant K, indicating no net change in the concentrations of reactants and products. The energy levels of reactants and products are the same, leading to a ΔG of zero.
Gibbs free energy can also be calculated using specific equations. Under non-standard conditions, it is given by:
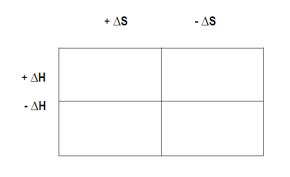
\[\Delta G = \Delta H - T \Delta S\]
where ΔH is the change in enthalpy, T is the temperature in Kelvin, and ΔS is the change in entropy. Standard conditions, denoted by a circle (°), imply a pressure of 1 atmosphere, a molarity of 1 molar, and a temperature of 25 degrees Celsius.
Additionally, Gibbs free energy under non-standard conditions can be expressed as:
\[\Delta G = \Delta G^\circ + RT \ln Q\]
where R is the gas constant (8.314 J/(mol·K)), T is the temperature in Kelvin, and Q is the reaction quotient (products over reactants). The relationship between Gibbs free energy under standard conditions and the equilibrium constant K is given by:
\[\Delta G^\circ = -RT \ln K\]
In summary, spontaneous reactions are characterized by a negative Gibbs free energy change, while non-spontaneous reactions have a positive change. Understanding these principles is vital for predicting the behavior of chemical reactions in various conditions.