1. On which derivative rule is integration by parts based?
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
12. Techniques of Integration
Integration by Parts
Problem 8.2.23
Textbook Question
9–40. Integration by parts Evaluate the following integrals using integration by parts.
23. ∫ x² sin(2x) dx
 Verified step by step guidance
Verified step by step guidance1
Identify the parts of the integral for integration by parts. Let \(u = x^{2}\) and \(dv = \sin(2x) \, dx\).
Compute the derivatives and integrals needed: find \(du = \frac{d}{dx}(x^{2}) \, dx = 2x \, dx\) and find \(v = \int \sin(2x) \, dx\).
Recall that \(\int \sin(ax) \, dx = -\frac{1}{a} \cos(ax) + C\), so here \(v = -\frac{1}{2} \cos(2x)\).
Apply the integration by parts formula: \(\int u \, dv = uv - \int v \, du\). Substitute the expressions for \(u\), \(v\), and \(du\).
Simplify the resulting integral \(\int v \, du\) and, if necessary, apply integration by parts again to evaluate it completely.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Integration by Parts
Integration by parts is a technique derived from the product rule of differentiation. It transforms the integral of a product of functions into simpler integrals using the formula ∫u dv = uv - ∫v du. Choosing u and dv wisely is crucial to simplify the integral effectively.
Recommended video:
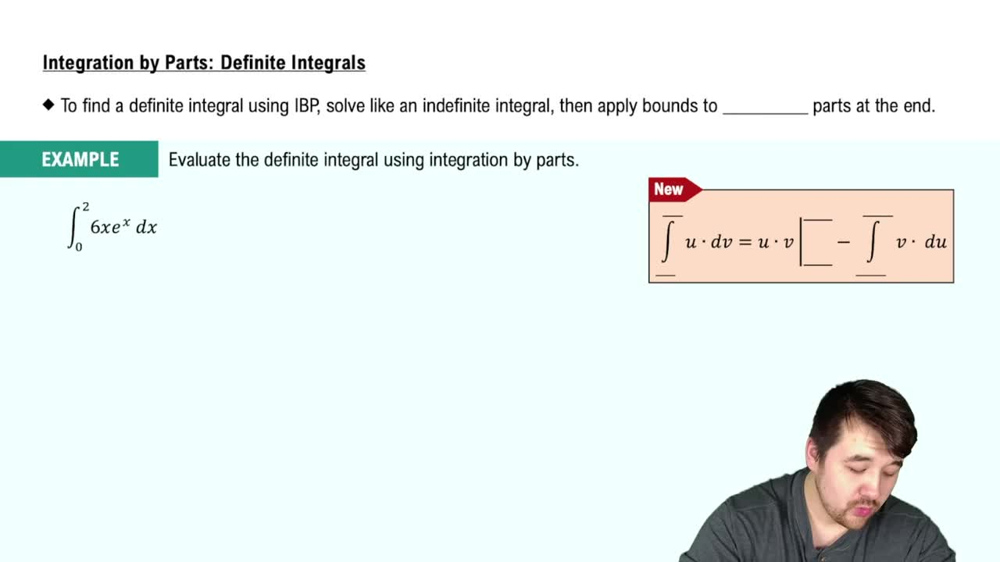
Integration by Parts for Definite Integrals
Choosing u and dv
Selecting which part of the integrand to assign as u and which as dv affects the ease of solving the integral. Typically, u is chosen as a function that simplifies when differentiated (like polynomials), and dv is chosen as a function that is easy to integrate (like trigonometric functions).
Recommended video:
Choosing a Convergence Test
Repeated Application of Integration by Parts
Some integrals, such as ∫x² sin(2x) dx, require applying integration by parts more than once. After the first application, the resulting integral may still be complex, necessitating a second iteration to fully evaluate the integral.
Recommended video:

Repeated Integration by Parts
Related Videos
Related Practice
Textbook Question
43
views


