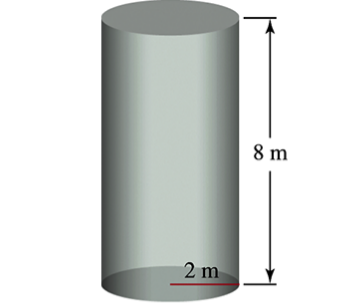
Emptying a cylindrical tank A cylindrical water tank has height 8 m and radius 2m (see figure).
b. Is it true that it takes half as much work to pump the water out of the tank when it is half full as when it is full? Explain.

Verified step by step guidance

1. Understand that the work required to pump water out of the tank depends on both the volume of water and the distance each layer of water must be lifted.
2. Set up the integral for work when the tank is full: consider a thin horizontal slice of water at height \(y\) with thickness \(dy\). The volume of this slice is the area of the base times \(dy\), which is \(\pi \times 2^2 \times dy = 4\pi dy\).
3. Calculate the weight of this slice by multiplying its volume by the density of water and gravity (these constants can be factored out). The distance the slice must be lifted is \$8 - y\( meters (from height \)y\( to the top of the tank). So, the work done on this slice is proportional to \)4\pi (8 - y) dy$.
4. Integrate this expression from \(y=0\) to \(y=8\) to find the total work when the tank is full: \(W_{full} = \int_0^8 4\pi (8 - y) dy\).
5. For the tank half full, repeat the process but integrate from \(y=0\) to \(y=4\): \(W_{half} = \int_0^4 4\pi (8 - y) dy\). Compare \(W_{half}\) to \(\frac{1}{2} W_{full}\) to determine if it takes half as much work to pump the water out when the tank is half full.

Key Concepts

Work Done by a Variable Force

Work in calculus is calculated as the integral of force over distance. When pumping water from a tank, the force varies with the weight of the water at different heights, requiring integration to sum the work done on each layer of water.

Volume and Weight of Water in a Cylinder

The volume of water in a cylindrical tank depends on the height of the water. Since weight is proportional to volume, the amount of work depends on how much water is present, which changes as the tank empties.

Distance Water is Pumped

The work depends not only on the amount of water but also on the distance each layer of water must be lifted. Water at the bottom must be pumped higher than water near the top, so the work is not simply proportional to the volume.