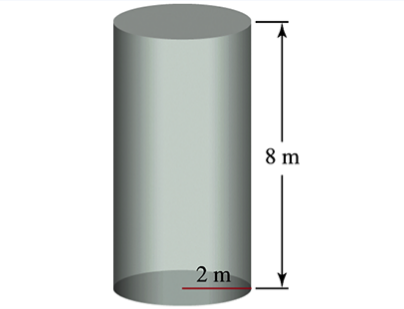
Emptying a cylindrical tank A cylindrical water tank has height 8 m and radius 2m (see figure).
a. If the tank is full of water, how much work is required to pump the water to the level of the top of the tank and out of the tank?

Verified step by step guidance

1. Identify the physical setup: The tank is a cylinder with height 8 m and radius 2 m, filled with water. We want to find the work required to pump all the water to the top of the tank and out.
2. Set up a coordinate system: Let the vertical axis y measure the height from the bottom of the tank (y=0) to the top (y=8). Consider a thin horizontal slice of water at height y with thickness dy.
3. Calculate the volume of the thin slice: The cross-sectional area of the tank is constant and given by the area of the circle, \(A = \pi \times (2)^2 = 4\pi\). The volume of the slice is \(dV = A \cdot dy = 4\pi \, dy\).
4. Determine the weight of the slice: The weight is the volume times the density of water times gravity. Let \(\rho\) be the density of water and \(g\) the acceleration due to gravity, so the weight is \(dW = \rho g \cdot dV = \rho g \cdot 4\pi \, dy\).
5. Calculate the work to pump the slice: The distance the slice must be lifted is from height y to the top at 8 m, so the distance is \((8 - y)\). The work to move this slice is \(dWork = (\text{weight}) \times (\text{distance}) = \rho g \cdot 4\pi (8 - y) \, dy\). Integrate this expression from \(y=0\) to \(y=8\) to find the total work.

Key Concepts

Work Done by a Variable Force

Work is the integral of force over distance. When pumping water from different depths, the force varies with the weight of the water being moved, and the distance changes depending on the water's height. Calculus helps sum these infinitesimal contributions to find total work.

Volume and Cross-Sectional Area of a Cylinder

The volume of water at a certain height in the cylindrical tank is found using the cross-sectional area (πr²) multiplied by the thickness of a water slice (dy). This allows calculation of the weight of each slice, essential for determining the force needed to pump it.

Density and Weight of Water

The weight of water is the product of its volume, density, and gravitational acceleration. Knowing the density of water (typically 1000 kg/m³) and gravity (9.8 m/s²) allows conversion from volume to force, which is necessary to compute the work done in pumping.