What is the polar equation of a circle of radius √(a²+b²) centered at (a, b)?
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
16. Parametric Equations & Polar Coordinates
Polar Coordinates
Problem 12.3.2
Textbook Question
Explain why the slope of the line θ=π/2 is undefined.
 Verified step by step guidance
Verified step by step guidance1
Recall that the slope of a line in the Cartesian plane is given by the ratio of the change in y to the change in x, which is \(\text{slope} = \frac{\Delta y}{\Delta x}\).
The line \(\theta = \frac{\pi}{2}\) in polar coordinates corresponds to all points where the angle from the positive x-axis is \$90^\circ$, which means the line is vertical.
A vertical line has the same x-coordinate for all points, so the change in x, \(\Delta x\), is zero along this line.
Since the slope formula involves division by \(\Delta x\), and here \(\Delta x = 0\), the slope expression becomes \(\frac{\Delta y}{0}\), which is undefined because division by zero is not defined in mathematics.
Therefore, the slope of the line \(\theta = \frac{\pi}{2}\) is undefined because it is a vertical line with no horizontal change.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slope of a Line
The slope of a line measures its steepness and is calculated as the ratio of the change in y to the change in x (rise over run). It indicates how much y changes for a unit change in x.
Recommended video:
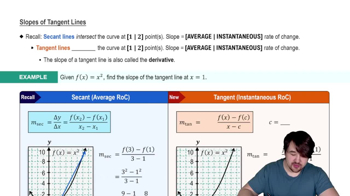
Slopes of Tangent Lines
Vertical Lines and Undefined Slope
Vertical lines have no horizontal change (Δx = 0), making the slope calculation involve division by zero, which is undefined. Therefore, vertical lines do not have a defined slope.
Recommended video:

Slopes of Tangent Lines
Angle θ = π/2 in Polar Coordinates
The line θ = π/2 in polar coordinates corresponds to the vertical line x = 0 in Cartesian coordinates. Since it is vertical, its slope is undefined due to zero horizontal displacement.
Recommended video:
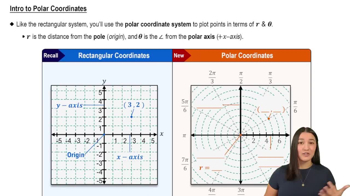
Intro to Polar Coordinates

 5:32m
5:32mWatch next
Master Intro to Polar Coordinates with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
22
views
