Determine if the function f ( x ) f\left(x\right) f ( x ) is continuous and/or differentiable at x = 3 x=3 x = 3 .

So in this problem, we are asked to determine if the function f of x is continuous and or differentiable at x equals 3. And notice we have this piecewise function over here. So how can we solve this? Well, the a good place to start whenever you're dealing with these kinds of problems is to first see whether or not if the function is continuous at our value of interest, x equals 3. So what I'm going to do to determine this is set the left side of this piecewise function equal to the right side at an x value of 3, and see if the two sides are equal. Now, if I do this for the left side, that's x squared, so we're going to have 3 squared. And if I do this for the right side, that's gonna be 27 over this x value of 3. Now 3 squared, that's equal to 9, and 27 over 3 is also 9. 9 does equal 9, so this function is continuous at an x value of 3. That means at this point, I would not have to pick up my pencil. I could trace this all in one since the two sides are equal. But now let's see whether or not the function is differentiable. So to determine this, well, what we need to now do is see if the derivatives on both sides are going to be equal to each other. And to figure this out, well, we can use the definition of a derivative, which is f prime of x is going to be the limit as h approaches 0 for the function f of x plus h minus or yes minus f of x all divided by h. So let's go ahead and use this equation over here. So what I'm going to do is use this this definition of a derivative and apply it to both of these functions and then set them equal to each other at an x value of 3. So let's start with x squared. Well, I can find the derivative of x squared by using the definition of a derivative. So we're going to have the limit as h approaches 0 of x+2, that's f of x+h, minus our function x squared, all divided by h. Now whenever using this equation, I can't just take 0 and plug it in for h because that would be dividing by 0, But what I can do is try to simplify things to get that h on bottom to cancel. So I can expand out x +hsquared to get x squared plus 2xh+hsquared, then we'll have minus x squared all divided by h. Now from here I can cancel the x squared since we have a positive and a negative and I can also factor out an h from both of these terms. So we're going to keep this limit as h approaches 0 since we have not applied it yet and then we're going to have h times 2x minus the remaining h we have there all divided by h, in which case we can cancel these h's, meaning we're just going to have 2x minus h. Now applying this limit right here, and I forgot to write the limit out front here since we haven't applied it yet, but applying this limit to 2x minus h, it's going to just take 0 and put it in for h, meaning all we're going to have left is 2x, and that's our derivative. So we're going to have 2x on the left side, but now we need to figure out what the right side is. Well, the right side we're trying to find the derivative of this equation. So I'm going to go ahead and use the definition of a derivative again on what we have over here. So for this, we're going to have that f prime of x is equal to the limit as h approaches 0, and then we're going to have 27 over x+H, the minus 27 over x, all divided by h. So we have kind of a complicated looking function that we have right here, but the way that we can try to simplify this, so we don't have this h on bottom, meaning we won't divide by 0, is we're going to see if we can somehow clear these fractions that we have on top. And the way that I'm going to do that is by multiplying this top with a common multiple that I see in the denominators here, and I'm going to multiply this on the top and the bottom to keep this fraction consistent. But what I can see is that that's going to be x plus h times x, because if I do that, this will get everything on bottom to cancel. So we'll have x times x plus h that I'll multiply everything by on top, and then I need to also multiply that by the bottom, x times x plus h. So what we're going to do here is distribute this in. So I'm going to keep this limit attached because this limit as h approaches 0 is going to stay on, but what I can see is that this will distribute into there, meaning we can cancel the x plus h's. So what we're going to have is just the x leftovers, we're gonna have 27 x on top and then minus, and then here, if we distribute this in, we can get those x's to cancel, meaning we're just going to have 27 times x+h, and then all of this is going to be divided by x times h, xh times x plus h. So this is what we end up getting. Now at this point, I still can't take my 0 and just plug it in for h, but what I can do is distribute this 27 into these parentheses to try to simplify things farther. So again, we're still gonna have this limit attached, because we haven't applied it yet, but we're going to have 27 x, and then I can distribute this negative 27 into these parentheses. So I have minus 27 x, and then minus 27 h, and then all of that's going to be divided by x h times x plus h. I'm not gonna quite distribute anything here because I I want this h to stay on the outside so we can cancel it. Now what I can see on top is that these 27 x's are gonna cancel each other since we have a positive and a negative. So all we're gonna be left with is this negative 27 h. But notice if we just have a negative 27 h on top, then we have this x h on bottom, notice that h would cancel with that one. So this is just being multiplied on in both cases. So that will reduce. So this is going to end up becoming the limit as h approaches 0 of negative 27 all over x times x plus h. And since we did get an h to cancel on bottom, I can now try applying this limit to what we have. So what I'm going to do is take this 0 here, I'm going to replace it with that h, meaning we're going to have negative 27 on top, and then on bottom, we're going to have x times x plus 0. Now, x times x plus 0 that's just the same thing as x squared. So we get negative 27 over x squared as our derivative. So that's going to be the right side of this, of what we have here. So this is going to be negative 27 over x squared, and then I need to check this at an x value of 3 because we're trying to figure out whether or not this is differentiable. So if I plug 3 into the left side, and then I can take 3 and plug it in to the right side. So we're gonna have 3 squared on bottom, and 2 times 3 is 6, and then we'll have negative 27 over 3 squared which is 9, and then negative 27 divided by 9 would be negative 3, and obviously 6 does not equal negative 3. So therefore this function is continuous, but it is not differentiable, and that would be the solution to this problem. So that is how you can solve these types of problems, where you need to figure out whether a function is continuous, and whether or not the function is also differentiable. So that's the solution here. Hope you found this video helpful, and let's go ahead and move on.

2. Intro to Derivatives

Differentiability

Calculus

2. Intro to Derivatives

Differentiability

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Determine if the function $f\left(x\right)$ is continuous and/or differentiable at $x=3$ .

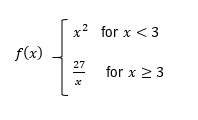
Continuous and non-differentiable

Continuous and differentiable

Discontinuous and non-differentiable

Discontinuous and differentiable

Verified step by step guidance

Step 1: To determine if the function is continuous at x=3, check if the left-hand limit, right-hand limit, and the function value at x=3 are equal. Calculate the left-hand limit as x approaches 3 from the left using f(x) = x^2.

Step 2: Calculate the right-hand limit as x approaches 3 from the right using f(x) = 27/x. Compare this limit with the left-hand limit calculated in Step 1.

Step 3: Evaluate the function value at x=3 using f(x) = 27/x. Compare this value with the limits calculated in Steps 1 and 2 to determine continuity.

Step 4: To determine differentiability at x=3, check if the derivative from the left and the derivative from the right are equal. Calculate the derivative of f(x) = x^2 at x=3 using the definition of the derivative.

Step 5: Calculate the derivative of f(x) = 27/x at x=3 using the definition of the derivative. Compare this derivative with the one calculated in Step 4 to determine differentiability.

5:02m

Watch next

Master Determining Differentiability Graphically with a bite sized video explanation from Patrick

Start learning

Struggling with Calculus?

Determine if the function f(x)f\left(x\right)f(x) is continuous and/or differentiable at x=3x=3x=3.

Watch next

Determine if the function $f\left(x\right)$ is continuous and/or differentiable at $x=3$ .