Introduction to Trigonometric Functions: Videos & Practice Problems

Angles can be measured in degrees and radians, with a full circle equating to 360 degrees or $2\pi$ radians. To convert between these units, use the formulas: multiply by $\pi$/$180$ for degrees to radians, and $180$/$\pi$ for radians to degrees. Trigonometric functions like sine, cosine, and tangent relate angles to side lengths in right triangles, represented by the ratios: sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, and tangent = opposite/adjacent, remembered by SOHCAHTOA.

Converting between Degrees & Radians

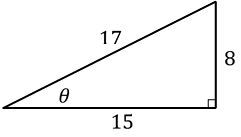
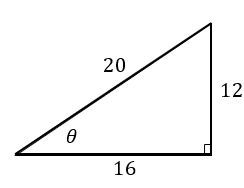
Understanding angles is essential in geometry, and two common units for measuring angles are degrees and radians. A full circle measures 360 degrees, while in radians, a full circle is represented as \(2\pi\) radians. The concept of radians is based on the relationship between the radius of a circle and its circumference. Specifically, one radian is defined as the angle created when the length of the arc is equal to the radius of the circle, which is approximately 57 degrees.

To visualize this, if you take a circle with radius \(r\), the circumference can be calculated using the formula \(C = 2\pi r\). Thus, if you travel around the entire circumference, you complete \(2\pi\) radians. For practical purposes, angles in radians are often expressed in terms of fractions or multiples of \(\pi\). For instance, half a circle is \(\pi\) radians, a quarter circle is \(\frac{\pi}{2}\) radians, and three-quarters of a circle is \(\frac{3\pi}{2}\) radians.

To convert between degrees and radians, two key formulas are used. To convert degrees to radians, multiply the degree measure by \(\frac{\pi}{180}\). Conversely, to convert radians to degrees, multiply by \(\frac{180}{\pi}\). For example, to convert 120 degrees to radians, you would calculate:

\[120 \times \frac{\pi}{180} = \frac{120\pi}{180} = \frac{2\pi}{3} \text{ radians}\]

This shows that 120 degrees is equivalent to \(\frac{2\pi}{3}\) radians. Similarly, to convert an angle given in radians, such as \(\frac{6\pi}{5}\), to degrees, you would use the conversion factor \(\frac{180}{\pi}\):

\[\frac{6\pi}{5} \times \frac{180}{\pi} = \frac{6 \times 180}{5} = 216 \text{ degrees}\]

Thus, \(\frac{6\pi}{5}\) radians is equal to 216 degrees. Mastering these conversions is crucial for working with trigonometric functions and graphing in mathematics.

Convert the angle $540°$ from degrees to radians.

• A. $3\pi$ rad
• B. $\frac{3\pi}{2}$ rad
• C. $\frac{5\pi}{2}$ rad
• D. $4\pi$ rad

Answer: (A)

Convert the angle $-\frac{5\pi}{6}$ from radians to degrees.

• A. $-120\degree$
• B. $-150\degree$
• C. $-210\degree$
• D. $-240\degree$

Answer: (B)

Introduction to Trigonometric Functions

Trigonometric functions, commonly referred to as trig functions, are essential in mathematics as they establish a relationship between angles and the side lengths of right triangles. The three primary trig functions are sine, cosine, and tangent, each defined as specific ratios of the sides of a right triangle.

To understand these functions, consider a right triangle with an angle denoted as θ. The sine of θ (sin θ) is calculated as the ratio of the length of the side opposite the angle to the length of the hypotenuse (the longest side). This can be expressed as:

$$\sin(θ) = \frac{\text{opposite}}{\text{hypotenuse}}$$

For example, if the opposite side measures 3 units and the hypotenuse measures 5 units, then:

$$\sin(θ) = \frac{3}{5}$$

Next, the cosine of θ (cos θ) is determined by the ratio of the length of the adjacent side (the side next to the angle) to the hypotenuse:

$$\cos(θ) = \frac{\text{adjacent}}{\text{hypotenuse}}$$

Using the same triangle, if the adjacent side measures 4 units, then:

$$\cos(θ) = \frac{4}{5}$$

Lastly, the tangent of θ (tan θ) is the ratio of the opposite side to the adjacent side:

$$\tan(θ) = \frac{\text{opposite}}{\text{adjacent}}$$

In our example, this would be:

$$\tan(θ) = \frac{3}{4}$$

To help remember these relationships, the mnemonic SOHCAHTOA is often used. This stands for:

• SOH: Sine = Opposite / Hypotenuse
• CAH: Cosine = Adjacent / Hypotenuse
• TOA: Tangent = Opposite / Adjacent

Additionally, it is important to note that the tangent function can also be expressed in terms of sine and cosine:

$$\tan(θ) = \frac{\sin(θ)}{\cos(θ)}$$

For example, if we know that:

$$\sin(θ) = \frac{3}{5}$$ and $$\cos(θ) = \frac{4}{5}$$

Then:

$$\tan(θ) = \frac{\frac{3}{5}}{\frac{4}{5}} = \frac{3}{4}$$

When solving problems involving trigonometric functions, it is crucial to reference the correct angle. For instance, when calculating the cosine of an angle, ensure that you identify the adjacent side relative to that specific angle. This attention to detail is vital for accurate calculations.

In summary, mastering the definitions and relationships of sine, cosine, and tangent through the SOHCAHTOA mnemonic will greatly enhance your understanding and application of trigonometric functions in various mathematical contexts.

Given the right triangle below, evaluate $\cos\theta$.

• A. $\cos\theta=\frac{8}{17}$
• B. $\cos\theta=\frac{8}{15}$
• C. $\cos\theta=\frac{15}{17}$
• D. $\cos\theta=\frac{15}{8}$

Answer: (C)

Given the right triangle below, evaluate $\tan\theta$.

• A. $\tan\theta=\frac35$
• B. $\tan\theta=\frac45$
• C. $\tan\theta=\frac43$
• D. $\tan\theta=\frac34$

Answer: (D)

Trig Values in Quadrants II, III, & IV

Understanding the trigonometric values of angles in different quadrants is essential for mastering trigonometry. The key concept is that the sine, cosine, and tangent values of angles in quadrants 2, 3, and 4 can be derived from the reference angles in quadrant 1, with adjustments made for the signs based on the quadrant's characteristics.

In quadrant 1, all trigonometric values are positive. As we move to quadrant 2, for example, the angle of 150 degrees has a reference angle of 30 degrees. The cosine and sine values remain the same as those of the reference angle, but the cosine becomes negative because it corresponds to the x-coordinate, which is negative in this quadrant. Thus, the values for 150 degrees are:

Cosine: \( -\frac{\sqrt{3}}{2} \), Sine: \( \frac{1}{2} \), Tangent: \( -\frac{\sqrt{3}}{3} \).

In quadrant 3, consider the angle of 225 degrees, which has a reference angle of 45 degrees. Here, both the sine and cosine values are negative, while the tangent remains positive since it is the ratio of sine to cosine:

Cosine: \( -\frac{\sqrt{2}}{2} \), Sine: \( -\frac{\sqrt{2}}{2} \), Tangent: \( 1 \).

Moving to quadrant 4, the angle of 300 degrees has a reference angle of 60 degrees. In this quadrant, the cosine is positive while the sine is negative, leading to the following values:

Cosine: \( \frac{1}{2} \), Sine: \( -\frac{\sqrt{3}}{2} \), Tangent: \( -\frac{\sqrt{3}}{3} \).

To remember which trigonometric functions are positive in each quadrant, a helpful mnemonic is "All Students Take Calculus." This indicates that in quadrant 1, all functions are positive; in quadrant 2, only sine is positive; in quadrant 3, only tangent is positive; and in quadrant 4, only cosine is positive.

By understanding these relationships and the adjustments needed for each quadrant, students can effectively navigate the unit circle and apply trigonometric principles to various problems.

Trig Values in Quadrants II, III, & IV Example 1

Understanding reference angles is essential for determining the trigonometric values in different quadrants of the unit circle. Each quadrant has specific signs for sine, cosine, and tangent based on the mnemonic "All Students Take Calculus," which indicates which functions are positive in each quadrant.

In Quadrant 2, we analyze angles of 135 degrees and 120 degrees, which correspond to reference angles of 45 degrees and 60 degrees, respectively. The trigonometric values for these reference angles are:

• For 135 degrees:
  • sin(135°) =   \(\frac{\sqrt{2}}{2}\)
  • cos(135°) =   \(-\frac{\sqrt{2}}{2}\)
  • tan(135°) =   \(-1\)
• For 120 degrees:
  • sin(120°) =   \(\frac{\sqrt{3}}{2}\)
  • cos(120°) =   \(-\frac{1}{2}\)
  • tan(120°) =   \(-\frac{\sqrt{3}}{3}\)

In this quadrant, only sine is positive, so cosine and tangent are negative.

Moving to Quadrant 3, we consider angles of 210 degrees and 240 degrees, with reference angles of 30 degrees and 60 degrees. The corresponding trigonometric values are:

• For 210 degrees:
  • sin(210°) =   \(-\frac{1}{2}\)
  • cos(210°) =   \(-\frac{\sqrt{3}}{2}\)
  • tan(210°) =   \( \frac{\sqrt{3}}{3}\)
• For 240 degrees:
  • sin(240°) =   \(-\frac{\sqrt{3}}{2}\)
  • cos(240°) =   \(-\frac{1}{2}\)
  • tan(240°) =   \( \sqrt{3}\)

In this quadrant, only tangent is positive, so sine and cosine are negative.

Finally, in Quadrant 4, we examine angles of 330 degrees and 315 degrees, which have reference angles of 30 degrees and 45 degrees. The trigonometric values are:

• For 330 degrees:
  • sin(330°) =   \(-\frac{1}{2}\)
  • cos(330°) =   \(\frac{\sqrt{3}}{2}\)
  • tan(330°) =   \(-\frac{\sqrt{3}}{3}\)
• For 315 degrees:
  • sin(315°) =   \(-\frac{\sqrt{2}}{2}\)
  • cos(315°) =   \(\frac{\sqrt{2}}{2}\)
  • tan(315°) =   \(-1\)

In this quadrant, only cosine is positive, so sine and tangent are negative.

By understanding the reference angles and the signs of the trigonometric functions in each quadrant, you can efficiently determine the values needed for various angles on the unit circle. Practice these concepts to reinforce your understanding and application of trigonometric functions.

Identify what angle, $\theta$ , satisfies the following conditions.
$\sin\theta=\frac12$; $\tan\theta$ < $0$

• A. 30°
• B. 150°
• C. 60°
• D. 300°

Answer: (B)

Identify what angle, $\theta$ , satisfies the following conditions.
$\cos\theta=\frac{\sqrt3}{2}$; $\sin\theta$ < $0$

• A. 30°
• B. 60°
• C. 120°
• D. 330°

Answer: (D)

Identify what angle, $\theta$ , satisfies the following conditions.
$\tan\theta=-1$; $\cos\theta$ > $0$

• A. 45°
• B. 135°
• C. 315°
• D. 330°

Answer: (C)

Trig Values in Quadrants II, III, & IV Example 2

To effectively fill in a unit circle, it's essential to understand the key angles and their corresponding trigonometric values. The unit circle is divided into four quadrants, each containing specific angle measures in both degrees and radians. The primary quadrantal angles are 0 degrees (0 radians), 90 degrees (π/2 radians), 180 degrees (π radians), and 270 degrees (3π/2 radians), culminating in a full rotation of 360 degrees (2π radians).

For each of these quadrantal angles, the coordinates on the unit circle are as follows: at 0 degrees, the point is (1, 0); at 90 degrees, it is (0, 1); at 180 degrees, it is (-1, 0); and at 270 degrees, it is (0, -1). The tangent values, calculated as y/x, yield 0 for 0 degrees and 180 degrees, while the tangent is undefined for 90 degrees and 270 degrees.

In the first quadrant, the common angles of 30 degrees (π/6 radians), 45 degrees (π/4 radians), and 60 degrees (π/3 radians) are crucial. The reference angle for these is 30 degrees. To find the corresponding angles in the other quadrants, we can use the following methods:

• In the second quadrant, subtract the reference angle from 180 degrees: 180° - 30° = 150° (5π/6 radians).
• In the third quadrant, add the reference angle to 180 degrees: 180° + 30° = 210° (7π/6 radians).
• In the fourth quadrant, subtract the reference angle from 360 degrees: 360° - 30° = 330° (11π/6 radians).

These angles share a common denominator of 6 in their radian measures, which can aid in memorization. The tangent values for these angles can be derived from the sine and cosine values, which are based on the coordinates of the points on the unit circle. In the first quadrant, the sine and cosine values are all positive, while in the other quadrants, the signs change based on the quadrant:

• Quadrant 2: Only sine is positive.
• Quadrant 3: Only tangent is positive.
• Quadrant 4: Only cosine is positive.

Using the mnemonic "All Students Take Calculus," one can easily remember which trigonometric functions are positive in each quadrant. For example, in quadrant 2, the sine values remain positive while cosine and tangent values are negative. This pattern continues for the other quadrants, allowing for a systematic approach to filling in the unit circle.

By practicing this process repeatedly, students can become proficient in identifying angles, their corresponding coordinates, and the associated trigonometric values on the unit circle. This foundational knowledge is essential for further studies in trigonometry and calculus.

Here’s what students ask on this topic:

How do you convert degrees to radians?

To convert degrees to radians, you use the formula:

$\frac{\pi }{180}$

Multiply the angle in degrees by $\frac{\pi }{180}$. For example, to convert 120 degrees to radians:

$\frac{120\pi }{180}=\frac{2\pi }{3}$

So, 120 degrees is equal to $\frac{2\pi }{3}$ radians.

What is the SOHCAHTOA memory tool in trigonometry?

SOHCAHTOA is a mnemonic device used to remember the definitions of the trigonometric functions sine, cosine, and tangent:

• SOH: Sine = Opposite / Hypotenuse
• CAH: Cosine = Adjacent / Hypotenuse
• TOA: Tangent = Opposite / Adjacent

This tool helps you recall that sine is the ratio of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side in a right triangle.

How do you convert radians to degrees?

To convert radians to degrees, you use the formula:

$\frac{180}{\pi }$

Multiply the angle in radians by $\frac{180}{\pi }$. For example, to convert $\frac{6\pi }{5}$ radians to degrees:

$\frac{6\pi }{5}*\frac{180}{\pi }=\frac{1080}{5}=\; 216$

So, $\frac{6\pi }{5}$ radians is equal to 216 degrees.

What are the trigonometric functions of common angles in the unit circle?

In the unit circle, common angles and their trigonometric functions are:

• 0° (0 radians): sin(0) = 0, cos(0) = 1, tan(0) = 0
• 30° ($\frac{\pi }{6}$ radians): sin(30°) = $\frac{1}{2}$, cos(30°) = $\frac{\mathrm{\surd 3}}{2}$, tan(30°) = $\frac{1}{\mathrm{\surd 3}}$
• 45° ($\frac{\pi }{4}$ radians): sin(45°) = $\frac{\mathrm{\surd 2}}{2}$, cos(45°) = $\frac{\mathrm{\surd 2}}{2}$, tan(45°) = 1
• 60° ($\frac{\pi }{3}$ radians): sin(60°) = $\frac{\mathrm{\surd 3}}{2}$, cos(60°) = $\frac{1}{2}$, tan(60°) = $\mathrm{\surd 3}$
• 90° ($\frac{\pi }{2}$ radians): sin(90°) = 1, cos(90°) = 0, tan(90°) is undefined

What is the relationship between the trigonometric functions and the unit circle?

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. Trigonometric functions are closely related to the unit circle:

• Sine (sin): The y-coordinate of a point on the unit circle.
• Cosine (cos): The x-coordinate of a point on the unit circle.
• Tangent (tan): The ratio of the y-coordinate to the x-coordinate (sin/cos).

For an angle θ, the coordinates (cos(θ), sin(θ)) represent a point on the unit circle. This relationship helps visualize and understand the values of trigonometric functions for different angles.