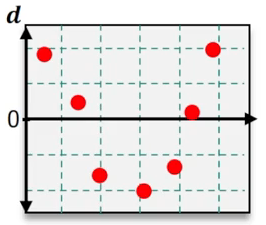
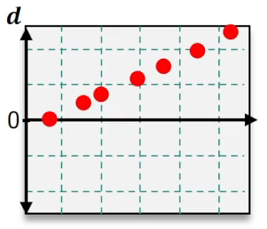
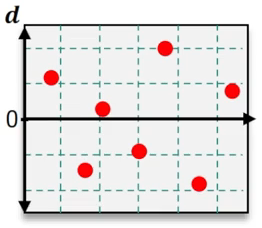
Which of the following residual plots suggest that a linear regression model is appropriate?

• A.
• B.
• C.
• D.

Answer: (C)

Verified step by step guidance

1. Step 1: Understand the purpose of residual plots in regression analysis. Residual plots are used to assess whether the assumptions of a linear regression model are valid. Specifically, they help determine if the residuals (errors) are randomly distributed and if the relationship between the independent and dependent variables is linear.
2. Step 2: Examine the residual plots provided. A residual plot that suggests a linear regression model is appropriate will show residuals scattered randomly around the horizontal axis (y = 0) without any discernible pattern.
3. Step 3: Identify patterns in the residual plots. For example, if the residuals form a curve, trend, or systematic pattern, this indicates that a linear model may not be appropriate. If the residuals are randomly distributed, this supports the use of a linear model.
4. Step 4: Compare the residual plots. In the images provided, look for the plot where the residuals are evenly scattered around the horizontal axis without forming a trend or systematic pattern.
5. Step 5: Conclude which residual plot suggests a linear regression model is appropriate based on the analysis. The correct plot will show no curvature, trend, or clustering of residuals, indicating that the linear regression assumptions are satisfied.