Inferences for Slope: Videos & Practice Problems

Hypothesis testing and confidence intervals for $\beta$, the slope of the population regression line, assess linear correlation between variables. The null hypothesis assumes $\beta =0$, indicating no linear relationship. Using TI-84 functions like LinRegTTest and LinRegTInt, students can calculate p-values and confidence intervals to determine if $\beta$ differs from zero. A p-value less than the alpha level (e.g., 0.05) or a confidence interval excluding zero provides evidence of significant linear association, crucial for interpreting regression analysis and understanding relationships in data.

Hypothesis Test for the Slope of a Regression Line

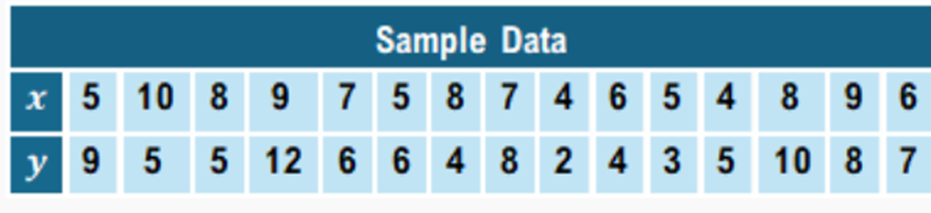
Understanding the relationship between two variables often involves analyzing the slope of the population's regression line, denoted as β. The slope β indicates the direction and strength of a linear correlation between variables. To determine if an observed linear trend in sample data is statistically significant and can be generalized to the population, a hypothesis test for β is conducted.

In this context, the null hypothesis (H₀) always states that there is no linear correlation between the variables, meaning the population slope β = 0. The alternative hypothesis (H_a) depends on the research question: it can be two-sided (β ≠ 0) if testing for any linear relationship, or one-sided (β > 0 or β < 0) if testing for a positive or negative correlation specifically.

For example, consider an economic study examining the relationship between advertising spending and product sales (measured in thousands of dollars). To test the claim that no linear relationship exists at a significance level of α = 0.05, the hypotheses are set as:

H₀: β = 0
H_a: β ≠ 0

Using statistical software or a graphing calculator like the TI-84, the data for advertising spending and sales are input into separate lists. The LinRegTTest function performs the hypothesis test for the slope β. This function calculates the test statistic t and the corresponding p-value, which quantifies the probability of observing the data assuming the null hypothesis is true.

When the p-value is less than the significance level α, the null hypothesis is rejected, indicating sufficient evidence to conclude that the population slope β is not zero. This implies a statistically significant linear correlation between the variables.

In the advertising and sales example, the calculated p-value was approximately 3.4 × 10⁻⁶, which is much smaller than 0.05. Therefore, the null hypothesis is rejected, supporting the conclusion that advertising spending and product sales have a significant linear relationship.

This process highlights the importance of hypothesis testing in regression analysis to validate whether observed trends in sample data reflect true relationships in the population. Mastery of these concepts enables accurate interpretation of correlation and causation in various fields such as economics, biology, and social sciences.

Using the sample data below, run a hypothesis test on $\beta$ to see if there is evidence that there is a positive correlation between $x$ and $y$ with $\alpha =0.01$.

• A. Reject $H_0$ and conclude that there is a positive correlation between $x$ and $y$ and that $\beta>0$.
• B. Fail to reject $H_0$ since there is enough evidence to suggest $\beta>0$, but not enough evidence to suggest positive linear correlation between $x$ and $y$.
• C. Fail to reject $H_0$ since there is not enough evidence to suggest $\beta>0$ and not enough evidence to suggest positive linear correlation between $x$ and $y$.
• D. Reject $H_0$ since there is not enough evidence to suggest $\beta>0$ and not enough evidence to suggest positive linear correlation between $x$ and $y$.

Answer: (C)

Hypothesis Test for the Slope of a Regression Line Example 1

When investigating the relationship between website loading speed (measured in seconds) and the number of visits per minute, it is essential to determine if a linear correlation exists. This can be analyzed through a hypothesis test on the slope (β) of the population regression line. The null hypothesis (H₀) assumes no linear correlation, meaning the slope β equals zero (β = 0). The alternative hypothesis (H_a) tests whether there is a linear correlation, so β ≠ 0, indicating the slope is nonzero.

To perform this test, data for website speed and visits are entered into two lists (L1 for speed and L2 for visits) on a statistical calculator such as the TI-84. Using the WinRegTTest function, the test is set up with the x-list as L1, the y-list as L2, frequency as 1, and the alternative hypothesis as β ≠ 0. This function calculates the test statistic and the p-value.

The p-value obtained from the test is approximately 0.003. Comparing this to the significance level α = 0.1, since p-value < α, the null hypothesis is rejected. This indicates sufficient evidence to conclude that the slope β is not zero, confirming a statistically significant linear correlation between website loading speed and the number of visits per minute.

This process highlights the importance of hypothesis testing in regression analysis to determine the presence of meaningful relationships between variables. Understanding how to set up and interpret these tests allows for informed decisions based on data trends, especially in fields like web design where user engagement metrics are critical.

Hypothesis Test for the Slope of a Regression Line Example 2

When analyzing the relationship between shipping time and customer satisfaction, it is essential to understand how changes in one variable affect the other. In this context, the shipping manager wants to determine if longer shipping times lead to lower customer satisfaction ratings. This involves performing a hypothesis test on the slope (β) of the population regression line, which quantifies the linear relationship between shipping time (independent variable) and customer satisfaction (dependent variable).

The null hypothesis (H₀) assumes no linear relationship exists, meaning the slope β equals zero (β = 0). The alternative hypothesis (H_a) reflects the manager’s suspicion that increased shipping time decreases satisfaction, implying a negative slope (β < 0). This setup tests for a negative linear correlation between the two variables.

Using statistical software or a graphing calculator, the shipping time data is entered as the independent variable list (L1), and customer satisfaction ratings as the dependent variable list (L2). The linReg t-test function is then applied to calculate the test statistic and p-value, specifying the alternative hypothesis as β < 0.

The resulting p-value is approximately 2.4 × 10⁻⁴, which is significantly less than the chosen significance level α = 0.05. Since the p-value < α, the null hypothesis is rejected, providing strong evidence that the slope β is negative. This confirms a statistically significant negative linear correlation between shipping time and customer satisfaction.

Given this evidence, it is reasonable for the shipping manager to invest in researching more efficient shipping methods. Reducing shipping time is likely to improve customer satisfaction, which can enhance overall service quality and customer retention.

This analysis highlights the importance of hypothesis testing in regression to understand relationships between variables. By formulating clear hypotheses, inputting data correctly, and interpreting p-values relative to significance levels, one can make informed decisions based on statistical evidence.

Hypothesis Test for the Slope of a Regression Line Example 3

A quality control expert investigates whether increasing the frequency of machine servicing in a plant improves each machine's productivity. Data collected includes the number of times a machine is serviced per week and its corresponding daily productivity. To analyze this relationship, a linear regression approach is used, focusing on the regression line that models productivity as a function of service frequency.

The key step involves testing the slope (β) of the population regression line to determine if there is a statistically significant positive correlation between servicing frequency and productivity. The null hypothesis (H₀) states that there is no linear relationship, meaning β = 0. The alternative hypothesis (H₁) posits that β > 0, indicating that more frequent servicing leads to higher productivity.

Using statistical software or a graphing calculator, the data is input with the number of services as the independent variable (x) and productivity as the dependent variable (y). A linear regression t-test is performed at a significance level (α) of 0.05. The test yields a p-value of approximately 0.09, which exceeds the alpha threshold. This result means there is insufficient evidence to reject the null hypothesis, so the data does not support a positive linear correlation between servicing frequency and productivity.

From the regression output, the sample regression line is determined as:

\[ y = 22.43 + 1.23x \]

Here, 22.43 represents the y-intercept, indicating the estimated productivity when no servicing occurs, and 1.23 is the slope, representing the estimated increase in productivity for each additional service per week. Despite the positive slope, the lack of statistical significance suggests that this observed increase could be due to random variation rather than a true effect.

Consequently, the company does not have sufficient evidence to conclude that increasing the frequency of machine servicing will effectively boost productivity. This analysis highlights the importance of hypothesis testing in validating whether observed trends in sample data reflect genuine relationships in the population.

Confidence Interval for the Slope of a Regression Line

Constructing a confidence interval for β, the slope of the population regression line, provides a powerful method to assess whether two variables exhibit a linear relationship. This approach complements hypothesis testing by estimating a range of plausible values for the slope rather than testing a specific claim directly. When analyzing the relationship between variables such as hours spent on lesson plans and students' average test scores, a confidence interval can reveal whether the slope differs significantly from zero, indicating linear correlation.

To create a 95% confidence interval for the slope β, the confidence level (C) is set at 0.95. Using statistical tools like the TI-84 calculator, the LinRegTInt function efficiently computes this interval. The process begins by entering the independent variable data (e.g., hours) into list L1 and the dependent variable data (e.g., test scores) into list L2. After selecting the LinRegTInt function from the calculator’s test menu, ensure the correct lists are assigned for x and y, the frequency is set to 1, and the confidence level matches the desired value (0.95 for 95%). Executing the calculation yields the confidence interval for the slope.

For example, if the 95% confidence interval for β is approximately $\backslash (0.93\backslash )$ to $\backslash (1.5\backslash )$, this interval does not include zero. Since a slope of zero would indicate no linear correlation, the exclusion of zero from the interval suggests strong evidence of a linear relationship between the variables. In other words, we can be 95% confident that the true slope is not zero, confirming a statistically significant linear association.

This method highlights the importance of confidence intervals in regression analysis, providing an intuitive range for the slope parameter and reinforcing conclusions about correlation. By understanding and applying confidence intervals for β, students can better interpret the strength and significance of linear relationships in data, enhancing their analytical skills in statistics and data science.

Using the sample data below, create a confidence interval for $\beta$ to see if there is evidence that there is a positive correlation between $x$ and $y$ with $\alpha =0.01$.

• A. $\left(-0.75,1.37\right)$; there is not enough evidence to suggest that there is a positive correlation between $x$ and $y$ with $\alpha=0.01$.
• B. $\left(-0.75,1.37\right)$; there is enough evidence to suggest that there is a positive correlation between $x$ and $y$ with $\alpha=0.01$.
• C. $\left(0.75,1.37\right)$; there is not enough evidence to suggest that there is a positive correlation between $x$ and $y$ with $\alpha=0.01$.
• D. $\left(0.75,1.37\right)$; there is enough evidence to suggest that there is a positive correlation between $x$ and $y$ with $\alpha=0.01$.

Answer: (A)

Confidence Interval for the Slope of a Regression Line Example 4

An advertising executive is investigating whether increasing the length of a television advertisement, measured in minutes, leads to higher sales, measured in thousands of dollars. To analyze this relationship, a confidence interval for the slope β of the population regression line is constructed with a significance level α = 0.1, corresponding to a 90% confidence level.

Using statistical software or a TI-84 calculator, the data for ad length and sales are input into lists (L1 for length and L2 for sales). The LinRegTInt function is then used to calculate the confidence interval for the slope. This function requires specifying the x-list (ad length), y-list (sales), frequency (default 1), and the confidence level (0.9 for 90%). The resulting confidence interval for β is approximately from 0.1 to 0.3.

This interval is crucial because it only contains positive values, indicating a positive linear relationship between ad length and sales. Since the entire confidence interval is above zero, we can be 90% confident that the true slope β is positive. This means that as the length of the advertisement increases, sales tend to increase as well.

Therefore, there is sufficient statistical evidence to conclude that longer television ads are associated with higher sales. The advertising executive should consider producing longer ads to potentially boost product sales. This conclusion is supported by the positive confidence interval for the slope, confirming a positive linear correlation between advertisement length and sales revenue.

Confidence Interval for the Slope of a Regression Line Example 5

When analyzing the relationship between commute time and employee satisfaction, it is essential to understand how to construct and interpret a confidence interval for the slope of the population regression line. In this context, the slope, denoted as β, represents how changes in commute time affect employee satisfaction levels. Using a significance level of α = 0.1, the confidence level for the interval is calculated as 1 - α = 0.9, or 90%. This means we are 90% confident that the true slope lies within the calculated interval.

To compute this confidence interval, one can use statistical software or a graphing calculator by inputting the commute times as the independent variable (x-values) and employee satisfaction scores as the dependent variable (y-values). The process involves selecting the appropriate regression t-interval function, specifying the data lists, and setting the confidence level to 0.90. The resulting confidence interval for the slope might be approximately $(-0.16,\; -0.11)$, indicating the range within which the true slope is likely to fall.

Interpreting this interval is crucial: since both bounds are negative, it provides strong evidence of a negative linear relationship between commute time and employee satisfaction. In other words, as commute time increases, employee satisfaction tends to decrease. This negative correlation is statistically significant at the 90% confidence level, meaning there is only a 10% chance that this observed relationship is due to random variation.

Understanding this relationship allows organizations to make informed decisions. For example, if longer commutes are shown to reduce satisfaction, companies might implement policies such as remote work options to improve employee well-being. The confidence interval's negativity confirms that such interventions are justified based on the data.

In summary, constructing a confidence interval for the slope of a regression line helps quantify the strength and direction of the relationship between variables. A negative confidence interval for the slope indicates a negative correlation, guiding practical decisions to enhance outcomes like employee satisfaction.

Confidence Interval for the Slope of a Regression Line Example 6

A film critic is investigating whether there is a linear relationship between movie length and the score a film receives. To analyze this, data from a random sample of movies, including their lengths and scores, is collected. The goal is to determine the regression line that best fits this sample data and to assess if the slope of the population regression line, denoted as β, indicates a significant association between movie length and score.

To find the regression line, the confidence interval for the slope is first calculated, as it provides essential information for constructing the regression equation. Given a significance level α = 0.01, the confidence level is 1 - α = 0.99. Using statistical software or a calculator such as the TI-84, the movie length data is entered as the independent variable (x) and the movie score data as the dependent variable (y). The linear regression t-interval function is then used to compute the confidence interval for the slope.

The resulting 99% confidence interval for the slope ranges approximately from -52 to +30. Alongside this, the regression equation is determined as:

\( \hat{y} = 97 - 11x \)

where 97 is the y-intercept and -11 is the slope of the sample regression line. This equation models the predicted movie score based on its length.

To decide whether further research is warranted, the confidence interval for the slope is examined. Since the interval includes zero, it suggests that the true slope β of the population regression line could be zero. A slope of zero implies no linear correlation between movie length and score. Therefore, there is insufficient evidence to conclude a significant linear relationship exists, and further research based on this data is not justified.

This analysis highlights the importance of confidence intervals in regression analysis, as they provide insight into the reliability and significance of the estimated slope. Understanding that a confidence interval containing zero indicates a lack of significant linear association helps in making informed decisions about the relationship between variables.

Here’s what students ask on this topic:

What is the null hypothesis when testing the slope of a population regression line?

The null hypothesis in testing the slope $\beta$ of a population regression line is that there is no linear relationship between the two variables. This means the slope of the population regression line is zero, expressed as $H{0}_{}:\beta =0$. This hypothesis assumes that changes in the explanatory variable do not predict changes in the response variable. Rejecting this null hypothesis suggests evidence of a linear association between the variables.

How do you use a TI-84 calculator to perform a hypothesis test for the slope of a regression line?

To perform a hypothesis test for the slope $\beta$ using a TI-84 calculator, first enter your data into lists (e.g., $L1$ for the explanatory variable and $L2$ for the response variable). Then, press STAT, navigate to the TESTS menu, and select LinRegTTest (option F). Ensure the x list and y list are correctly set, frequency is 1, and choose the alternative hypothesis (e.g., $\beta \ne 0$ for two-tailed). Calculate to get the test statistic and p-value. If the p-value is less than your significance level (commonly 0.05), reject the null hypothesis, indicating a significant linear relationship.

What does a confidence interval for the slope tell us about the relationship between two variables?

A confidence interval for the slope $\beta$ provides a range of plausible values for the true slope of the population regression line. For example, a 95% confidence interval means we are 95% confident that the true slope lies within this range. If the interval does not include zero, it suggests a significant linear relationship between the variables. Conversely, if zero is within the interval, we do not have enough evidence to conclude a linear association. This method complements hypothesis testing by providing an estimate range rather than just a yes/no decision.

How do you construct a confidence interval for the slope using a TI-84 calculator?

To construct a confidence interval for the slope $\beta$ on a TI-84, first input your data into lists (e.g., $L1$ and $L2$). Press STAT, go to the TESTS menu, and select LinRegTInt (option G). Confirm the x and y lists, set frequency to 1, and enter your confidence level (e.g., 0.95 for 95%). Calculate to get the interval. This interval estimates the range where the true slope likely falls. If zero is not in this interval, it indicates a significant linear relationship.

What does it mean if the p-value from a slope hypothesis test is less than the significance level?

If the p-value from a hypothesis test for the slope $\beta$ is less than the significance level (commonly $\alpha =\; 0.05$), it means there is strong evidence against the null hypothesis $H{0}_{}:\beta =0$. Therefore, we reject the null hypothesis and conclude that the slope is significantly different from zero. This indicates a statistically significant linear relationship between the explanatory and response variables in the population.