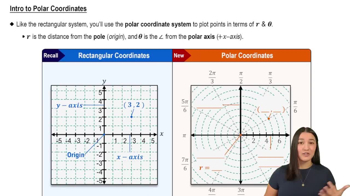
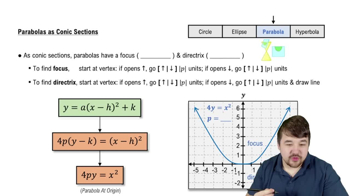
53–56. Eccentricity-directrix approach Find an equation of the following curves, assuming the center is at the origin. Sketch a graph labeling the vertices, foci, asymptotes (if they exist), and directrices. Use a graphing utility to check your work.
An ellipse with vertices (0, ±9) and eccentricity ¼