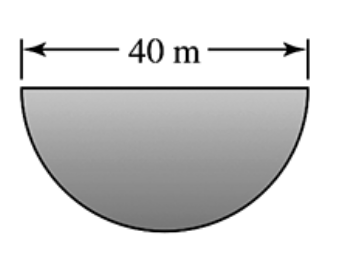
46–50. Force on dams The following figures show the shapes and dimensions of small dams. Assuming the water level is at the top of the dam, find the total force on the face of the dam.

Verified step by step guidance

1. Step 1: Understand the problem setup. The dam face is shaped like a semicircle with a diameter of 40 meters, and the water level is at the top of the dam. We need to find the total force exerted by the water on this curved surface.
2. Step 2: Recall that the force exerted by a fluid on a surface is given by the integral of pressure times the area element. The pressure at a depth \( y \) below the water surface is \( p(y) = \rho g y \), where \( \rho \) is the density of water and \( g \) is the acceleration due to gravity.
3. Step 3: Set up a coordinate system with \( y = 0 \) at the water surface (top of the dam) and positive \( y \) increasing downward. The semicircle extends from \( y = 0 \) to \( y = 20 \) meters (since radius \( r = 20 \) m).
4. Step 4: Express the width of the dam at depth \( y \) as a function of \( y \). For a semicircle of radius \( r \), the half-width at depth \( y \) is \( x = \sqrt{r^2 - (r - y)^2} \). The full width is then \( 2x = 2 \sqrt{r^2 - (r - y)^2} \).
5. Step 5: Write the force integral as \( F = \int_0^{20} p(y) \times \text{width}(y) \, dy = \int_0^{20} \rho g y \times 2 \sqrt{r^2 - (r - y)^2} \, dy \). This integral represents the total hydrostatic force on the dam face.

Key Concepts

Hydrostatic Pressure

Hydrostatic pressure is the pressure exerted by a fluid at rest due to the force of gravity. It increases linearly with depth and is calculated as P = ρgh, where ρ is fluid density, g is acceleration due to gravity, and h is the depth below the surface. Understanding this helps determine the pressure distribution on the dam face.

Force on a Surface Due to Fluid Pressure

The total force exerted by a fluid on a submerged surface is found by integrating the pressure over the area. Since pressure varies with depth, the force is the integral of pressure times differential area. This concept is essential for calculating the total force on the curved dam face.

Calculus Integration for Area and Force

Calculus integration is used to sum infinitesimal forces over the dam's surface, especially when the shape is curved. Setting up the integral with appropriate limits and variables allows precise calculation of total force by accounting for varying pressure and surface geometry.