Change of variables Use the change of variables u³ = 𝓍² ― 1 to evaluate the integral ∫₁³ 𝓍∛(𝓍²―1) d𝓍 .
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
8. Definite Integrals
Substitution
Problem 7.1.29
Textbook Question
29–62. Integrals Evaluate the following integrals. Include absolute values only when needed.
∫₀³ (2x - 1) / (x + 1) dx
 Verified step by step guidance
Verified step by step guidance1
Start by examining the integral \( \int_0^3 \frac{2x - 1}{x + 1} \, dx \). Notice that the integrand is a rational function where the degree of the numerator is equal to the degree of the denominator.
Perform polynomial division to simplify the integrand. Divide \( 2x - 1 \) by \( x + 1 \) to express the integrand as a polynomial plus a proper fraction. This will help in integrating more easily.
After division, rewrite the integral as \( \int_0^3 \left( \text{quotient} + \frac{\text{remainder}}{x + 1} \right) dx \). This separates the integral into simpler parts.
Integrate each part separately: the polynomial part integrates to a power function, and the fraction part integrates to a logarithmic function involving \( \ln|x + 1| \). Since \( x + 1 > 0 \) on \([0,3]\), absolute value is not necessary here.
Finally, apply the Fundamental Theorem of Calculus by evaluating the antiderivative at the upper and lower limits \( x=3 \) and \( x=0 \), then subtract to find the value of the definite integral.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Integration of Rational Functions
This involves integrating functions expressed as the ratio of two polynomials. Techniques often include algebraic manipulation such as polynomial division or partial fraction decomposition to simplify the integrand before integrating.
Recommended video:
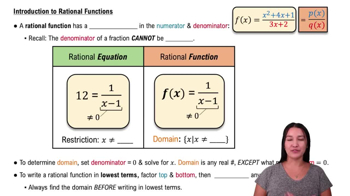
Intro to Rational Functions
Definite Integrals and Limits of Integration
Definite integrals calculate the net area under a curve between two specified points. The limits of integration (here, 0 to 3) define the interval over which the function is integrated, resulting in a numerical value.
Recommended video:

Definition of the Definite Integral
Use of Absolute Values in Logarithmic Integrals
When integrating functions that lead to logarithmic expressions, absolute values ensure the argument of the logarithm remains positive. Absolute values are included only when the domain of the function requires it to maintain validity.
Recommended video:

Integration Using Partial Fractions
Related Videos
Related Practice
Textbook Question
115
views


