Slope of a Line: Videos & Practice Problems

The slope of a line, represented by $m$, measures its steepness and is calculated as the rise over run, or the change in $y$ divided by the change in $x$ ($\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}$). Slopes can be positive, negative, zero (horizontal lines, $y=\mathrm{constant}$), or undefined (vertical lines, $x=\mathrm{constant}$). Understanding slope is essential for analyzing linear equations and graph behavior in algebra and coordinate geometry.

Finding the Slope of a Line

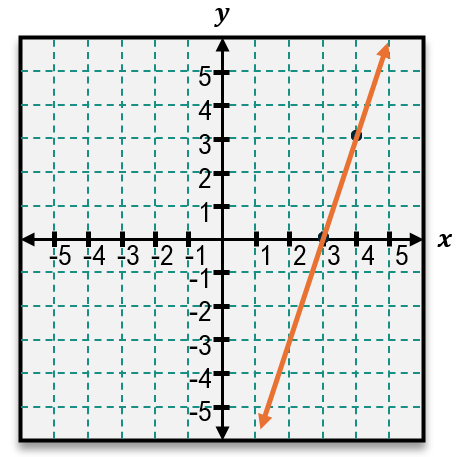
The slope of a line is a fundamental concept in understanding the characteristics of linear equations. Represented by the letter m, the slope measures the steepness or incline of a line. It is calculated by dividing the vertical change, known as the rise, by the horizontal change, called the run. This relationship can be expressed simply as slope = rise/run.

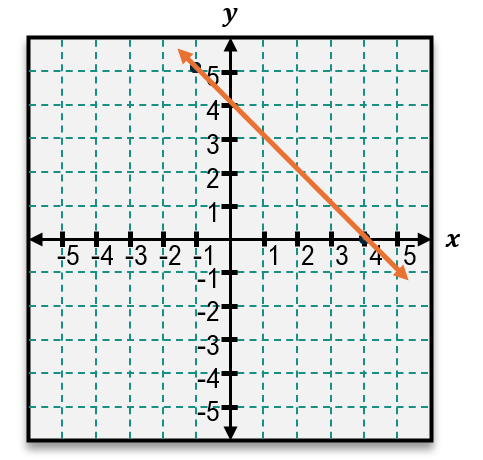
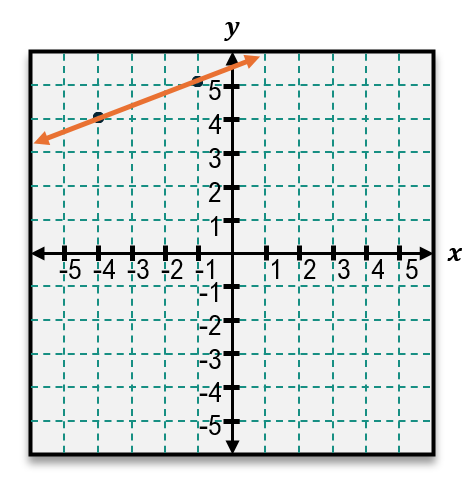
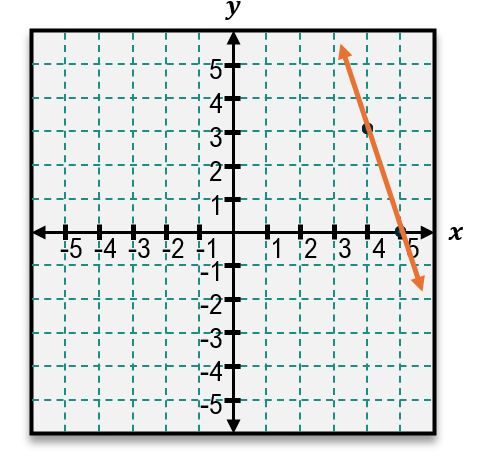
When given a graph, the slope can be found by identifying two points on the line and counting the units moved vertically and horizontally between them. For example, if the line rises 3 units and runs 1 unit to the right, the slope is 3/1, which equals 3. This indicates a relatively steep line.

More formally, the slope is calculated using the coordinates of two points, (x₁, y₁) and (x₂, y₂), on the line. The formula for slope is:

\[m = \frac{y_2 - y_1}{x_2 - x_1}\]

Here, the numerator represents the change in the y-values (rise), and the denominator represents the change in the x-values (run). The symbol Δ (delta) is often used to denote change, so slope can also be written as:

\[m = \frac{\Delta y}{\Delta x}\]

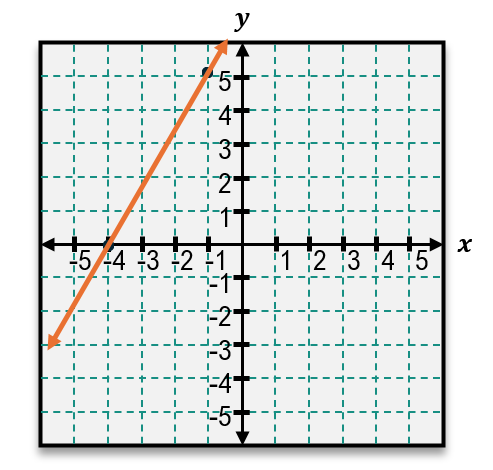
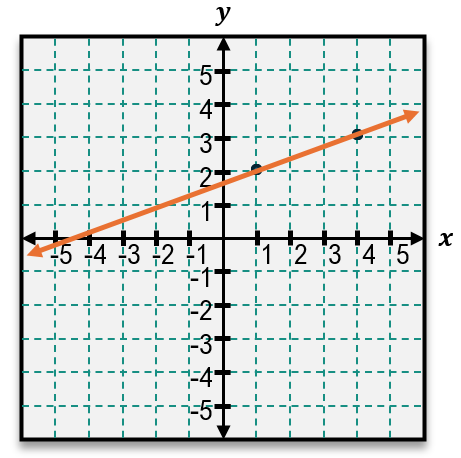
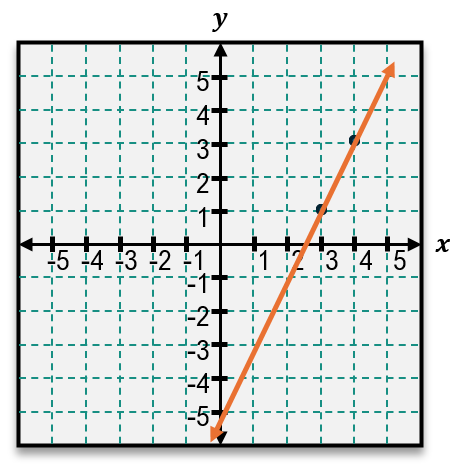
For instance, if the points are (-1, 0) and (0, 3), the slope calculation would be:

\[m = \frac{3 - 0}{0 - (-1)} = \frac{3}{1} = 3\]

It is important to note that the order of subtraction must be consistent; however, it does not matter which point is chosen as the first or second, as long as the same order is used for both numerator and denominator.

When only two points are given without a graph, the same formula applies. For example, given points (1, 2) and (4, 5), the slope is:

\[m = \frac{5 - 2}{4 - 1} = \frac{3}{3} = 1\]

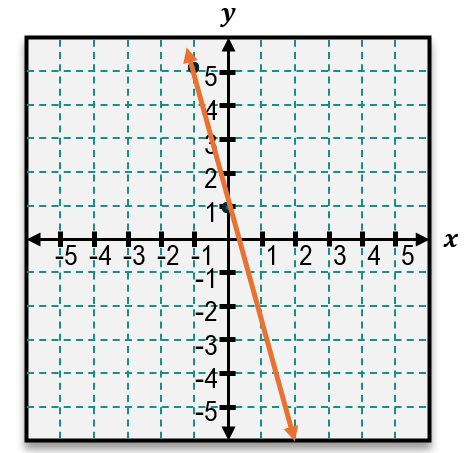
This slope of 1 indicates a less steep line compared to a slope of 3. Understanding how to calculate slope from either a graph or coordinate points is essential for analyzing linear relationships and predicting behavior of lines in various contexts.

Finding the Slope of a Line Example 1

To find the slope of a line given two points, it is essential to understand that the slope represents the ratio of the vertical change (rise) to the horizontal change (run) between those points. The slope formula is expressed as:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

Here, \((x_1, y_1)\) and \((x_2, y_2)\) are the coordinates of the two points on the line. The order of points does not affect the calculation as long as the differences are consistent.

For example, consider the points \((-2, -5)\) and \((4, 3)\). Assigning \(x_1 = -2\), \(y_1 = -5\), \(x_2 = 4\), and \(y_2 = 3\), substitute these values into the slope formula:

\[ m = \frac{3 - (-5)}{4 - (-2)} = \frac{3 + 5}{4 + 2} = \frac{8}{6} \]

Simplify the fraction by dividing numerator and denominator by their greatest common divisor, which is 2:

\[ m = \frac{8 \div 2}{6 \div 2} = \frac{4}{3} \]

This means the slope of the line is \(\frac{4}{3}\), indicating that for every 3 units moved horizontally (run), the line rises 4 units vertically (rise).

To verify this slope, one can select any point on the line and check if moving 3 units horizontally corresponds to a 4-unit vertical change. This confirms the accuracy of the slope calculation and reinforces the understanding of slope as a measure of steepness.

Finding the Slope of a Line Example 2

To determine the slope of a line given two points, it is essential to understand that the slope represents the ratio of the vertical change (rise) to the horizontal change (run) between those points. The slope formula is expressed as:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

where \((x_1, y_1)\) and \((x_2, y_2)\) are the coordinates of the two points on the line. The order of points does not affect the final slope value, as long as the subtraction is consistent.

For example, consider two points: the first point at \((-4, 4)\) and the second point at \((4, 0)\). Applying the slope formula, calculate the difference in the y-values (rise):

\[ y_2 - y_1 = 0 - 4 = -4 \]

and the difference in the x-values (run):

\[ x_2 - x_1 = 4 - (-4) = 4 + 4 = 8 \]

Thus, the slope is:

\[ m = \frac{-4}{8} = -\frac{1}{2} \]

This means the line falls one unit vertically for every two units it moves horizontally to the right, indicating a negative slope.

To verify this slope, one can use the rise-over-run method on the graph. Starting from a point on the line, moving down one unit (rise of -1) and right two units (run of 2) should land on another point on the line, confirming the slope of \(-\frac{1}{2}\).

Understanding how to calculate and interpret slope is fundamental in coordinate geometry, as it describes the steepness and direction of a line. The slope formula provides a straightforward method to quantify this characteristic using any two points on the line.

Finding the Slope of a Line Example 3

To determine the slope of a line given two points, we use the fundamental concept that slope represents the ratio of the vertical change (rise) to the horizontal change (run) between those points. Mathematically, the slope \( m \) is calculated using the formula:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

Here, \((x_1, y_1)\) and \((x_2, y_2)\) are the coordinates of the two points on the line. The order of points does not affect the final slope value, as long as the subtraction is consistent.

For example, consider the points \((-4, 4)\) and \((4, 0)\). Applying the slope formula:

\[ m = \frac{0 - 4}{4 - (-4)} = \frac{-4}{8} = -\frac{1}{2} \]

This result means the line decreases by 1 unit vertically for every 2 units it moves horizontally to the right, indicating a negative slope.

To verify this slope, you can use the rise-over-run method directly on the graph. Starting from a point on the line, move down 1 unit (rise of -1) and right 2 units (run of 2). If this movement lands on another point on the line, the slope calculation is confirmed.

Understanding slope as the ratio of vertical change to horizontal change is essential in analyzing linear relationships, graphing lines, and solving problems involving rates of change.

Find the slope of the following line.
$\frac{1}{2}x-\frac{2}{3}y=4$

• A. $\frac34$
• B. $-\frac34$
• C. $-6$
• D. $-8$

Answer: (A)

Find the slope of the following line.
$0.5x+0.2y=3$

• A. $\frac25$
• B. $\frac65$
• C. $\frac52$
• D. $-\frac52$

Answer: (D)

Types of Slope

Understanding slopes is essential in mathematics, as it describes the steepness of a line or hill, represented as the ratio of the vertical change (rise) to the horizontal change (run). Mathematically, this is expressed as the formula:

\[\text{slope} = \frac{\Delta y}{\Delta x}\]

Slopes can be categorized into four types: positive, negative, zero, and undefined. Each type provides insight into the behavior of the line.

Positive slopes occur when a line rises from left to right. For example, if you select two points on a line where the vertical change (rise) is 2 and the horizontal change (run) is 1, the slope would be:

\[\text{slope} = \frac{2}{1} = 2\]

Negative slopes, on the other hand, indicate a line that falls from left to right. If the rise is -1 (indicating a downward movement) and the run is 1, the slope calculation would yield:

\[\text{slope} = \frac{-1}{1} = -1\]

For horizontal lines, the slope is always zero because there is no vertical change. For instance, if the y-values remain constant at 2 while the x-values change, the slope is:

\[\text{slope} = \frac{0}{\Delta x} = 0\]

This indicates a perfectly flat line, which is represented by the equation:

\[y = c\]

where \(c\) is a constant value.

In contrast, vertical lines have an undefined slope because the horizontal change (run) is zero. For example, if both points lie on the line where \(x = 2\), the slope calculation would be:

\[\text{slope} = \frac{\Delta y}{0}\]

Since division by zero is undefined, we conclude that the slope of vertical lines is also undefined. The equation for vertical lines is expressed as:

\[x = a\]

where \(a\) is a constant value. Understanding these concepts is crucial for analyzing linear relationships in various mathematical contexts.

Graph a line with a slope of $0$ that passes through the point $(3,-2)$.

• A.
• B.
• C.
• D.

Answer: (D)

Which of the following graphs below represents the equation $x=3$?

• A.
• B.
• C.
• D.

Answer: (D)

Here’s what students ask on this topic:

What is the formula to calculate the slope of a line given two points?

The slope of a line, represented by $m$, is calculated using the formula $\frac{y{2}_{}-y{1}_{}}{x{2}_{}-x{1}_{}}$. This means you subtract the y-coordinate of the first point from the y-coordinate of the second point, then divide by the difference between the x-coordinates of the same points. This ratio, often called "rise over run," measures how steep the line is. It is important to keep the order consistent when subtracting to get the correct slope value.

How do you interpret positive, negative, zero, and undefined slopes on a graph?

Slopes describe the steepness and direction of a line. A positive slope means the line rises from left to right, indicating an increase in y as x increases. A negative slope means the line falls from left to right, showing a decrease in y as x increases. A zero slope corresponds to a horizontal line where y remains constant regardless of x, represented by $y=c$ where $c$ is a constant. An undefined slope occurs with vertical lines where x is constant, represented by $x=a$. Undefined slopes happen because division by zero occurs when calculating rise over run, which is mathematically undefined.

Can the slope of a line be zero or undefined, and what do these cases represent?

Yes, the slope of a line can be zero or undefined. A zero slope means the line is perfectly horizontal, so there is no vertical change as you move along the line. Mathematically, this is when $\frac{0}{\mathrm{\Delta x}}=\; 0$, where $\Delta x$ is the change in x. The equation of such a line is $y=k$, where $k$ is a constant. An undefined slope occurs when the line is vertical, meaning the change in x is zero, so the slope formula involves division by zero, which is undefined. The equation of a vertical line is $x=h$, where $h$ is a constant x-value.

Does the order of points affect the calculation of slope?

The order of points does not affect the value of the slope as long as you subtract the coordinates consistently. When calculating slope using two points $(x\_1,\; y\_1)$ and $(x\_2,\; y\_2)$, the formula is $\frac{y{2}_{}-y{1}_{}}{x{2}_{}-x{1}_{}}$. If you switch the points, you must subtract in the same order (second point minus first point) to get the same slope. Reversing the order of subtraction will change the sign of both numerator and denominator, resulting in the same slope value.

How do you find the slope of a line from a graph?

To find the slope from a graph, first identify two points on the line with clear coordinates. Then calculate the "rise" (vertical change) and the "run" (horizontal change) between these points. The slope is the ratio of rise over run, expressed as $\frac{}{}$. For example, if the line rises 3 units and runs 1 unit to the right, the slope is $\frac{1}{}=\; 3$. This method visually shows how steep the line is and whether it rises or falls as you move from left to right.