Introduction to Relations and Functions: Videos & Practice Problems

Relations connect inputs (x values) to outputs (y values) and can be represented as ordered pairs, tables, graphs, or equations. A function is a special relation where each input corresponds to exactly one output. The vertical line test helps identify functions on graphs: if any vertical line crosses more than one point, it's not a function. The domain is the set of all input values, and the range is the set of all output values. For continuous graphs, domain and range are expressed using interval notation, capturing all possible x and y values within specified bounds.

Intro to Relations and Functions

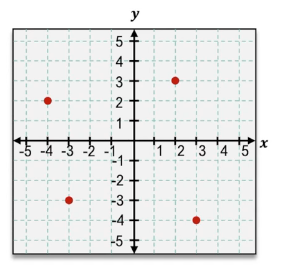
A relation is a fundamental concept in mathematics that describes a connection between inputs, often called x values, and outputs, known as y values. These connections are typically represented as sets of ordered pairs in the form \((x, y)\). To understand relations better, consider listing all the unique inputs and outputs from these pairs. For example, if you have ordered pairs like \((-2, 2)\), \((1, 1)\), \((3, -2)\), and \((1, 4)\), the inputs would be \(-2\), \$1\(, and \)3\(, while the outputs would be \)2\(, \)1\(, \)-2\(, and \)4\(. Visualizing these relations can be done by drawing arrows from each input to its corresponding output, illustrating how each value relates.

Functions are a special type of relation where each input is paired with exactly one output. This means no input value maps to more than one output. For instance, if you have ordered pairs like \)(-4, 2)\(, \)(-2, -1)\(, \)(1, 2)\(, and \)(3, 4)\(, each input corresponds to a single output, making this relation a function. In contrast, if an input like \)1\( maps to both \)1\( and \)4$, the relation is not a function. This distinction is crucial: all functions are relations, but not all relations are functions.

Relations and functions can be represented in various ways beyond ordered pairs. They can be shown as correspondences, tables, graphs, or equations, each providing a different perspective on how inputs and outputs relate. Understanding these representations helps in analyzing and interpreting mathematical relationships effectively.

Intro to Relations and Functions Example 1

To determine whether a relation is a function, it is essential to analyze how each input value (often represented as x) corresponds to output values (often represented as y). A function is defined as a relation where every input has exactly one output. This means no single input can map to multiple outputs.

For example, when given a table of values, start by listing the unique input values. Then, observe the outputs associated with each input. If any input corresponds to more than one output, the relation is not a function. For instance, if the input ½ maps to both 4 and 5, this violates the definition of a function because one input has multiple outputs.

Alternatively, when presented with a mapping diagram, even if the outputs are represented by letters or unknown values, you can still determine if the relation is a function by checking that each input arrow points to only one output. If every input connects to a single output, the relation qualifies as a function.

In summary, the key criterion for identifying a function is ensuring that each input value has at most one corresponding output value. This fundamental concept helps distinguish functions from general relations and is crucial for understanding mathematical mappings and their applications.

Vertical Line Test

A function is a special type of relation where each input corresponds to exactly one unique output. To quickly determine whether a relation represented on a graph is a function, the vertical line test is a useful method. This test involves imagining or drawing vertical lines across the graph. If any vertical line intersects the graph at more than one point, the relation is not a function. Conversely, if every vertical line touches the graph at only one point or none at all, the relation qualifies as a function.

For example, when examining a graph with discrete points, applying the vertical line test means checking each vertical line through the points. If no vertical line crosses more than one point, the graph represents a function. This confirms that each input (x-value) has a single output (y-value).

In the case of a smooth curve, which contains infinitely many points, the vertical line test remains effective. By drawing vertical lines at various positions, if any line intersects the curve at multiple points, it indicates that a single input corresponds to multiple outputs, disqualifying the relation as a function.

Thus, the vertical line test serves as a quick and reliable visual tool to distinguish functions from non-functions when dealing with graphs. It emphasizes the fundamental property of functions: each input must map to one and only one output.

State the inputs and outputs of the following relation. Is it a function?
$\{(-3,5),(0,2),(3,5)\}$

• A.
• B.
• C.
• D.

Answer: (C)

State the inputs and outputs of the following relation. Is it a function?
$\{(2,5),(0,2),(2,9)\}$

• A.
• B.
• C.
• D.

Answer: (B)

Vertical Line Test Example 2

To determine whether a graph represents a function, the vertical line test is a useful method. This test states that if a vertical line can be drawn anywhere on the graph and it intersects the graph at more than one point, then the graph is not a function. Conversely, if every vertical line drawn intersects the graph at most once, then the graph is indeed a function.

For example, consider three different graphs:

1. **Graph A**: When applying the vertical line test, any vertical line drawn across this graph intersects it at only one point. This consistent behavior confirms that Graph A is a function.

2. **Graph B**: In this case, a vertical line can be drawn that intersects the graph at multiple points. This indicates that Graph B does not satisfy the criteria for a function.

3. **Graph C**: Similar to Graph A, any vertical line drawn on Graph C intersects it at only one point. Thus, Graph C is also classified as a function.

In summary, Graphs A and C are functions, while Graph B is not. This understanding of the vertical line test is essential for identifying functions in various mathematical contexts.

Domain and Range

Understanding the domain and range is essential when working with relations and functions. The domain refers to the set of all possible input values, typically represented as the x-values, while the range is the set of all possible output values, or the y-values. These concepts help describe the behavior and limitations of functions and relations.

When given a relation as a list of ordered pairs, the domain consists of all the first elements (the x-values), and the range consists of all the second elements (the y-values). For example, if a relation is represented by the ordered pairs \((-2, 2)\), \((1, 1)\), \((3, -2)\), and \((4, 4)\), the domain is \(\{-2, 1, 3, 4\}\) and the range is \(\{2, 1, -2, 4\}\). This method is straightforward when dealing with discrete data points or tables.

However, when working with continuous functions represented by graphs, the domain and range often include infinitely many values. In such cases, it is more practical to express the domain and range using interval notation. Interval notation concisely describes all values between two endpoints, using brackets [ ] to include endpoints and parentheses ( ) to exclude them.

For instance, if a graph starts at \(x = -4\) with a solid dot (indicating inclusion) and extends indefinitely to the right, the domain is written as:

\[[-4, \infty)\]

Here, the bracket at \(-4\) means \(-4\) is included, while the parenthesis at infinity indicates that infinity is not a number and cannot be included.

Similarly, if the range of the graph starts at \(y = -2\) (included) and extends upward without bound, the range is:

\[[-2, \infty)\]

In summary, the domain encompasses all possible input values (x-values), and the range includes all possible output values (y-values). For discrete sets, list all values explicitly, and for continuous graphs, use interval notation to represent the domain and range efficiently. Mastering these concepts allows for a deeper understanding of functions and their behaviors across different representations.

Find the domain and range for each relation.
(A) $\{(-4,2),(-3,-5),(3,4),(5,-2)\}$

• A. Domain: $\left\lbrace-4,-3,3,5\right\rbrace$, Range: $\left\lbrace-4,-3,2,5\right\rbrace$
• B. Domain: $\left\lbrace-4,-3,3,5\right\rbrace$, Range: $\left\lbrace2,-5,4,-2\right\rbrace$
• C. Domain: ,$\left\lbrace-4,2,3,5\right\rbrace$ Range: $\left\lbrace2,-5,4,-2\right\rbrace$
• D. Domain: $\left\lbrace-4,-3,3,5\right\rbrace$, Range: $\left\lbrace5,-2,4,-5\right\rbrace$

Answer: (B)

Find the domain and range for each relation.
(B)

• A. Domain: $\left\lbrace-4,2,3\right\rbrace$, Range: $\left\lbrace2,3,-4\right\rbrace$
• B. Domain: $\left\lbrace-4,-3,2,3\right\rbrace$, Range: $\left\lbrace1,2,-3,3,-4\right\rbrace$$\left\lbrace2,-3,3,-4\right\rbrace$
• C. Domain: $\left\lbrace-4,-3,3\right\rbrace$, Range: $\left\lbrace2,-3,3,-4\right\rbrace$
• D. Domain: $\left\lbrace-4,-3,2,3\right\rbrace$, Range: $\left\lbrace2,-3,3,-4\right\rbrace$

Answer: (D)

Domain and Range Example 3

To determine the domain and range of a function from its graph, it is essential to understand that the domain represents all possible x-values for which the function is defined, while the range encompasses all possible y-values that the function attains. Expressing these sets in interval notation provides a clear and concise way to describe the extent of the function along the x- and y-axes.

For example, consider a graph where the function exists between certain x-values. If the graph starts just to the right of x = -4 (indicated by an open circle, meaning the value is not included) and extends to x = 2 (marked by a closed circle, meaning the value is included), the domain is expressed as \((-4, 2]\). This notation indicates that the function includes all x-values greater than -4 and up to and including 2.

Similarly, the range is determined by examining the vertical extent of the graph. If the y-values start just above y = -4 (with an open circle, so -4 is excluded) and extend up to and include y = 5 (closed circle), the range is \((-4, 5]\). This means the function takes on all y-values greater than -4 and up to 5.

In contrast, some graphs extend infinitely in one or both directions. For instance, if a graph continues indefinitely to the left and right, the domain includes all real numbers, expressed as \((-\infty, \infty)\). Likewise, if the graph extends infinitely upward and downward, the range also includes all real numbers, \((-\infty, \infty)\). This indicates there are no restrictions on the x- or y-values for the function.

Understanding how to interpret open and closed circles on a graph is crucial for correctly writing interval notation. Open circles denote values that are not included in the domain or range, while closed circles indicate inclusion. Additionally, recognizing when a graph extends infinitely helps identify when the domain or range is all real numbers.

By carefully analyzing the graph's horizontal and vertical extents and noting any open or closed endpoints, one can accurately determine the domain and range of a function and express them effectively using interval notation.

Here’s what students ask on this topic:

What is the difference between a relation and a function in algebra?

A relation in algebra is a set of ordered pairs that connects inputs (x-values) to outputs (y-values). It can be represented as ordered pairs, tables, graphs, or equations. A function is a special type of relation where each input corresponds to exactly one output. This means that in a function, no input value is paired with more than one output value. For example, if an input x = 1 maps to y = 2 and also y = 3, then the relation is not a function. However, if every input has only one output, it is a function. All functions are relations, but not all relations are functions. Understanding this distinction is fundamental in algebra and helps in analyzing mathematical models and graphs.

How do you use the vertical line test to determine if a graph represents a function?

The vertical line test is a quick method to determine if a graph represents a function. To use it, imagine drawing vertical lines (lines parallel to the y-axis) across the graph. If any vertical line intersects the graph at more than one point, the graph does not represent a function. This is because multiple intersections mean a single input (x-value) corresponds to multiple outputs (y-values), violating the definition of a function. Conversely, if every vertical line touches the graph at most once, the graph represents a function. This test is especially useful for continuous graphs and helps visually confirm the function property.

What are domain and range in the context of relations and functions?

In relations and functions, the domain is the set of all possible input values (x-values), while the range is the set of all possible output values (y-values). For example, if a function is given as a set of ordered pairs, the domain consists of all the x-values from those pairs, and the range consists of all the y-values. When dealing with continuous graphs, the domain and range are often expressed using interval notation to capture all values within certain bounds. For instance, if a graph starts at x = -4 and extends to infinity, the domain is written as $[-4,\infty )$. Understanding domain and range is essential for analyzing the behavior and limitations of functions.

How can relations be represented besides ordered pairs?

Relations can be represented in several ways besides ordered pairs. Common representations include tables, graphs, and equations. A table lists input-output pairs in rows, making it easy to see the relationship between x and y values. Graphs visually display the relation on the coordinate plane, showing how inputs correspond to outputs. Equations express the relation algebraically, defining y in terms of x or vice versa. Each representation offers a different perspective and can be useful depending on the problem context. Recognizing these forms helps in understanding and analyzing relations effectively.

Why is it important that each input in a function has only one output?

It is important that each input in a function has only one output because this uniqueness defines what a function is. If an input had multiple outputs, it would violate the fundamental property of functions, making it impossible to predict a single output for a given input. This property ensures consistency and allows functions to model real-world situations where one input corresponds to one result, such as calculating the area of a square given its side length. Without this rule, many mathematical tools and techniques used in calculus, algebra, and other fields would not work properly.