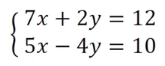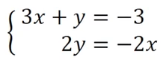Solving Systems of Linear Equations by Elimination: Videos & Practice Problems

The elimination method solves systems of linear equations by adding equations to eliminate one variable, often requiring multiplication to create equal and opposite coefficients. Equations must be in standard form, aligning terms like $x$ and $y$. Multiplying equations by constants adjusts coefficients to cancel variables, simplifying to solve for one variable, then substituting back. This method efficiently handles multivariable polynomials and coefficients, emphasizing understanding of terms, coefficients, and standard form for effective problem-solving in algebra.

Solving Systems of Linear Equations - Elimination

In solving systems of linear equations, the elimination method offers a systematic approach to simplify the process by eliminating one variable through addition. This method is particularly effective when equations are already in standard form, allowing for straightforward alignment of coefficients. The goal is to manipulate the equations so that when added together, one variable cancels out, making it easier to solve for the remaining variable.

To illustrate, consider the equations:

1. \(3x + 2y = 1\)

2. \(-x + y = 3\)

First, ensure both equations are in standard form, aligning the coefficients of \(x\), \(y\), and the constants vertically. If direct addition does not eliminate a variable, you may need to multiply one or both equations by a suitable number to create equal and opposite coefficients. For instance, multiplying the second equation by 3 yields:

1. \(3x + 2y = 1\)

2. \(-3x + 3y = 9\)

Now, adding these equations results in:

\((3x - 3x) + (2y + 3y) = 1 + 9\)

which simplifies to:

\(5y = 10\)

Thus, \(y = 2\).

With \(y\) determined, substitute this value back into either original equation to find \(x\). Using the second equation:

\(-x + 2 = 3\

Subtracting 2 from both sides gives:

\(-x = 1\

Therefore, \(x = -1\).

The solution to the system is the ordered pair \((-1, 2)\). To verify, substitute both values back into the original equations to ensure they satisfy both equations, confirming the solution's accuracy. The elimination method is a powerful tool for efficiently solving systems of equations, especially when dealing with larger coefficients or when equations are already aligned in standard form.

How to Multiply Equations in Elimination Method

In solving systems of equations using the elimination method, the key is to manipulate the coefficients of the variables so that one variable can be eliminated through addition or subtraction. This process can be broken down into several scenarios based on the relationships between the coefficients of the variables.

First, if the coefficients of either variable (x or y) are equal but have opposite signs, no additional steps are needed. For example, in the equations 7x + 13y = 12 and -7x + 2y = 18, the x coefficients cancel out directly, allowing you to proceed with solving for y.

In cases where the coefficients of a variable are equal and have the same sign, you must multiply one of the equations by -1 to create opposite signs. For instance, with the equations 5x + 7y = 17 and 6x + 7y = 12, multiplying the first equation by -1 results in -5x - 7y = -17. This adjustment allows for the y coefficients to cancel when the equations are added together.

Another scenario arises when the coefficients of a variable are factors of each other. For example, in the equations 12x - 5y = 24 and 3x - 2y = 6, the coefficients 12 and 3 are factors. To eliminate x, multiply the second equation by 4, resulting in 12x - 8y = 24. This allows for the x terms to cancel out, simplifying the equation to solve for y.

If none of these scenarios apply, a reliable method is to multiply each equation by the coefficient of the other equation's variable. For example, with the equations 6x + 2y = 10 and -4x + 3y = 15, you can multiply the first equation by 4 and the second by 6. This results in 24x + 8y = 40 and -24x + 18y = 90, allowing the x terms to cancel and enabling you to solve for y.

In summary, understanding the relationships between coefficients is crucial in the elimination method. By identifying the appropriate scenario, you can systematically eliminate variables and simplify the equations to find solutions efficiently.

Solving Systems of Linear Equations - Elimination Example 1

In solving systems of equations, one effective method is to eliminate a variable by strategically multiplying one or both equations. This approach allows for the coefficients of either the x or y variables to cancel out when the equations are added together. For example, consider the equations:

1. \(2x + 3y = 1\)

2. \(x - y = 3\)

To eliminate the x variable, we can analyze the coefficients. The coefficient of x in the first equation is 2, while in the second equation, it is 1 (implied). Since 2 is a multiple of 1, we can multiply the second equation by -2 to create opposite coefficients:

Multiplying the second equation by -2 gives:

\(-2(x - y) = -2(3)\)

which simplifies to:

\(-2x + 2y = -6\)

Now, we can rewrite the system:

1. \(2x + 3y = 1\)

2. \(-2x + 2y = -6\)

When we add these two equations, the x terms cancel:

\((2x - 2x) + (3y + 2y) = 1 - 6\

which simplifies to:

5y = -5

From this, we can solve for y:

y = -1

To find x, we can substitute y back into one of the original equations. However, the focus here is on the elimination process rather than fully solving the system.

Alternatively, we could choose to eliminate y instead. In this case, we notice that the coefficients of y in the two equations are 3 and -1, which are already opposites. We can multiply the second equation by 3:

Multiplying the second equation by 3 gives:

3(x - y) = 3(3)

which simplifies to:

3x - 3y = 9

Now, the system looks like this:

1. \(2x + 3y = 1\)

2. \(3x - 3y = 9\)

Adding these equations results in the y terms canceling out:

\((2x + 3x) + (3y - 3y) = 1 + 9\

which simplifies to:

5x = 10

From this, we can solve for x:

x = 2

Substituting x back into one of the original equations will yield the value of y, confirming that both methods lead to valid solutions. This flexibility in approach highlights the versatility of solving systems of equations through elimination.

Solving Systems of Linear Equations - Elimination Example 2

To solve a system of equations using the elimination method, we often need to manipulate the equations to facilitate the cancellation of one variable. Consider the equations:

1. \(5x + 3y = 10\)

2. \(-7x + 5y = 15\)

First, we analyze the coefficients of \(x\) and \(y\) to determine a suitable multiplication strategy. The coefficients \(5\) and \(-7\) are neither equal nor factors of each other, and they do not have opposite signs that would allow for immediate cancellation. Therefore, we can use a systematic approach by multiplying each equation by the coefficient of the other equation's variable.

In this case, we can multiply the first equation by \(7\) and the second equation by \(5\). This gives us:

Multiplying the first equation by \(7\):

\(7(5x + 3y) = 7(10)\)

Resulting in: \(35x + 21y = 70\)

Multiplying the second equation by \(5\):

\(5(-7x + 5y) = 5(15)\)

Resulting in: \(-35x + 25y = 75\)

Now we have the modified system:

1. \(35x + 21y = 70\)

2. \(-35x + 25y = 75\)

Next, we add these two equations together. The \(x\) coefficients cancel out:

\((35x - 35x) + (21y + 25y) = 70 + 75\)

This simplifies to:

\(46y = 145\)

To find \(y\), we divide both sides by \(46\):

\(y = \frac{145}{46}\)

Although this value for \(y\) is not a whole number, it is still valid. We can then substitute this value back into one of the original equations to solve for \(x\).

This method of multiplying equations by the coefficients of the other equation's variables is a reliable strategy for achieving cancellation and solving systems of linear equations effectively.

Use the elimination method to solve the following system of linear equations.
$2x+y=1$
$3x-y=4$

• A. $\left(-1,1\right)$
• B. $\left(1,1\right)$
• C. $\left(1,-1\right)$
• D. $\left(-1,-1\right)$

Answer: (C)

Use the elimination method to solve the following system of linear equations.
$10x-4y=5$
$5x-4y=1$

• A. $x=12,y=16$
• B. $x=16,y=12$
• C. $x=\frac34,y=\frac45$
• D. $x=\frac45,y=\frac34$

Answer: (D)

Here’s what students ask on this topic:

What is the elimination method for solving systems of linear equations?

The elimination method is a technique used to solve systems of linear equations by adding or subtracting the equations to eliminate one variable. This simplifies the system to a single-variable equation, which can be solved easily. The key steps include writing both equations in standard form, aligning terms vertically, and then adding or subtracting the equations so that one variable cancels out. Sometimes, you need to multiply one or both equations by constants to create equal and opposite coefficients for a variable. After eliminating one variable, you solve for the remaining variable and substitute back to find the other variable. This method is efficient, especially when equations have large coefficients or are already in standard form.

How do you decide what to multiply the equations by in the elimination method?

To decide what to multiply the equations by in the elimination method, examine the coefficients of the variables you want to eliminate. The goal is to create equal and opposite coefficients for one variable so they cancel when added. If the coefficients are already equal and opposite, no multiplication is needed. If they are equal but have the same sign, multiply one equation by $\mathrm{-1}$ to change the sign. If the coefficients are factors of each other, multiply the equation with the smaller coefficient by the quotient, possibly adding a negative sign. If none of these apply, multiply each equation by the other's coefficient for the variable you want to eliminate. This systematic approach ensures the variables cancel out effectively.

Why is it important to write equations in standard form before using the elimination method?

Writing equations in standard form is crucial for the elimination method because it aligns the variables and constants vertically, making it easier to add or subtract the equations correctly. Standard form means arranging each equation as $\mathrm{Ax}+\mathrm{By}=C$, where $A$, $B$, and $C$ are constants. This alignment helps you clearly see the coefficients of corresponding variables, which is essential for determining how to multiply the equations to eliminate one variable. Without standard form, terms might be scattered, increasing the chance of errors during addition or subtraction.

How do you solve for the remaining variable after eliminating one variable using the elimination method?

After eliminating one variable by adding or subtracting the equations, you will have a single-variable equation. To solve for the remaining variable, isolate it by performing algebraic operations such as addition, subtraction, multiplication, or division. For example, if you end up with an equation like $\mathrm{5y}=10$, divide both sides by 5 to find $y=2$. Once you have this value, substitute it back into one of the original equations to solve for the other variable. This substitution step completes the solution to the system.

What should you do if adding the equations does not eliminate a variable immediately?

If adding the equations does not eliminate a variable immediately, you need to multiply one or both equations by suitable constants to create equal and opposite coefficients for that variable. This often involves finding the least common multiple (LCM) of the coefficients of the variable you want to eliminate. Multiply each equation by the appropriate number so that the coefficients become equal in magnitude but opposite in sign. Then, add the equations to cancel out that variable. This step is essential to successfully apply the elimination method when coefficients are not already set up for elimination.