Regression analysis allows us to predict values of a dependent variable y based on an independent variable x, but these predictions are estimates subject to uncertainty. To quantify this uncertainty, prediction intervals are used, which provide a range within which we expect the actual y value to fall for a given x. Prediction intervals are similar to confidence intervals but specifically apply to predicted values from a regression model.
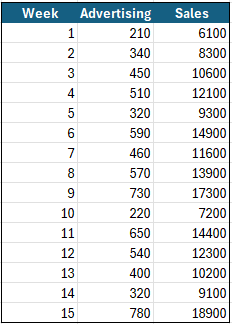
Consider a dataset where temperature and the number of bus riders show a strong linear relationship, indicated by a high coefficient of determination, \(R^2 = 0.874\), and a standard error of estimate, \(s_e = 2.97\). The regression line equation is given, allowing us to predict the number of riders for a specific temperature. For example, to predict the number of riders when the temperature is 35 degrees, substitute \(x_0 = 35\( into the regression equation:
\[\hat{y}_0 = b_0 + b_1 x_0\]where \)b_0\) is the intercept and \(b_1\) is the slope. This yields a predicted value \(\hat{y}_0 = 42.54\) riders.
Before constructing a 95% prediction interval for this prediction, two conditions must be verified: a strong linear correlation between variables (supported by the high \(R^2\) and scatterplot) and that the prediction point \(x_0\( lies within the range of observed data to avoid unreliable extrapolation.
The 95% prediction interval is calculated as:
\[\hat{y}_0 \pm t_{\alpha/2, n-2} \cdot s_e \sqrt{1 + \frac{1}{n} + \frac{(x_0 - \bar{x})^2}{\sum (x_i - \bar{x})^2}}\]Here, \)t_{\alpha/2, n-2}\) is the critical value from the t-distribution with \(n-2\) degrees of freedom, corresponding to the desired confidence level (e.g., 95% confidence means \(\alpha = 0.05\)). The term \(s_e\) is the standard error of the estimate, \(n\) is the number of data points, \(\bar{x}\) is the mean of the observed \(x\) values, and the denominator is the sum of squared deviations of \(x\) values from their mean.
To find the critical t-value, use statistical software or functions such as Excel’s T.INV.2T with inputs \(\alpha\) and degrees of freedom \(n-2\). For example, with \(n=13\) data points, the degrees of freedom are \$11\(, and the critical t-value for 95% confidence is approximately 2.201.
Calculate the mean of the \)x\( values (\(\bar{x}\)), the sum of the \)x\( values, and the sum of squares of the \)x\( values. Then compute the numerator \((x_0 - \bar{x})^2\) and the denominator \(\sum (x_i - \bar{x})^2\) to evaluate the fraction inside the square root.
After substituting all values, the margin of error \)E$ is computed. For the example, \(E \approx 6.914\). The prediction interval bounds are then:
\[\text{Lower bound} = \hat{y}_0 - E = 42.54 - 6.914 = 35.62\]\[\text{Upper bound} = \hat{y}_0 + E = 42.54 + 6.914 = 49.45\]This means we are 95% confident that the actual number of bus riders when the temperature is 35 degrees lies between approximately 35.62 and 49.45.
Understanding prediction intervals enhances the interpretation of regression predictions by accounting for variability and uncertainty inherent in real-world data. Utilizing tools like Excel simplifies the complex calculations involved, making it accessible to apply these concepts effectively in data analysis.