Introduction to Inverse Functions: Videos & Practice Problems

Understanding one-to-one functions is essential, where each output corresponds to a unique input, verified by the horizontal line test on graphs. Such functions have inverse functions, denoted as $f^{-1}$, which swap inputs and outputs, reversing the domain and range. This concept is crucial for analyzing relations and functions, including polynomials and their terms, ensuring clarity in function behavior and enabling deeper exploration of mathematical properties like exponents and coefficients.

One to One Functions

Understanding the concept of a one-to-one function builds upon the foundational idea of a function itself. A function is defined as a relation where each input value (x) corresponds to at most one output value (y). This means no input can map to multiple outputs. For example, if we consider a set of ordered pairs, each unique x-value is linked to a single y-value, ensuring the relation qualifies as a function.

Expanding on this, a one-to-one function (also called an injective function) requires that each output value is paired with at most one input value. In other words, no two different inputs share the same output. This property ensures a perfect pairing where each y-value corresponds to a unique x-value, establishing a one-to-one correspondence.

To determine if a function is one-to-one from ordered pairs or a correspondence diagram, observe the outputs: if any output repeats for different inputs, the function is not one-to-one. For instance, if the output value 2 is paired with both -4 and 1 as inputs, this violates the one-to-one condition. Conversely, if all outputs are unique, the function is one-to-one.

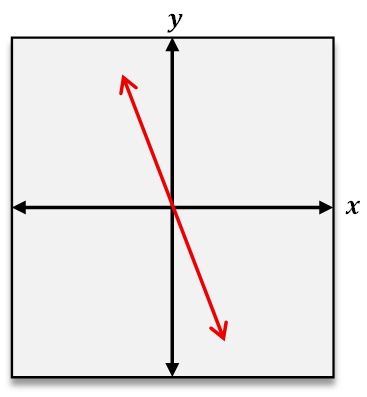
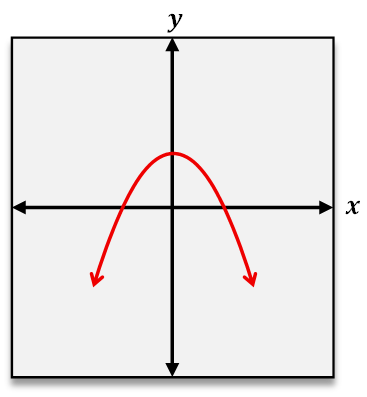
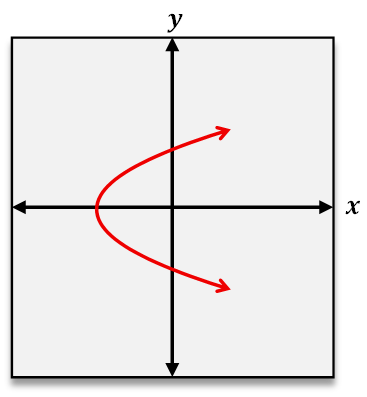
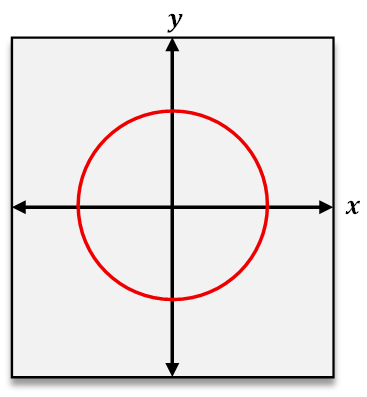
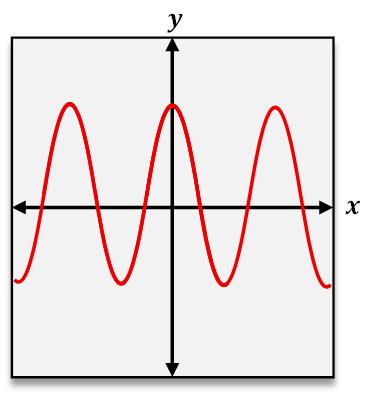
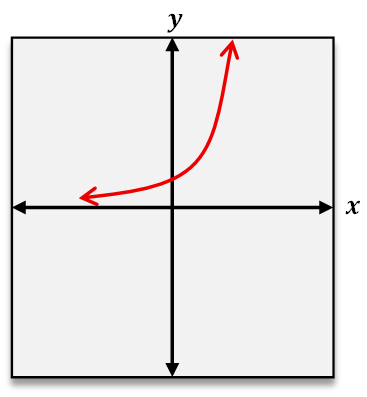
When analyzing functions graphically, the vertical line test helps confirm if a graph represents a function by checking that no vertical line intersects the graph at more than one point. To test if a function is one-to-one, the horizontal line test is used. This test involves drawing horizontal lines across the graph; if any horizontal line intersects the graph at more than one point, the function is not one-to-one. Passing the horizontal line test confirms that each output corresponds to a unique input, reinforcing the one-to-one nature of the function.

In summary, a one-to-one function ensures a unique pairing between inputs and outputs, which can be verified through ordered pairs by checking for repeated outputs or graphically by applying the horizontal line test. This understanding is crucial for deeper studies in functions, including inverse functions and their properties.

One to One Functions Example 1

To determine whether a graph represents a one-to-one function, it is essential to first verify if the graph is a function by applying the vertical line test. The vertical line test states that if any vertical line intersects the graph at more than one point, the graph does not represent a function. Once confirmed as a function, the horizontal line test can be used to check if the function is one-to-one. A one-to-one function passes the horizontal line test, meaning no horizontal line intersects the graph at more than one point.

For example, consider a parabola. Applying the vertical line test, no vertical line intersects the parabola at more than one point, confirming it is a function. However, when applying the horizontal line test, some horizontal lines intersect the parabola at two points, indicating it is not a one-to-one function.

Next, consider a linear graph. The vertical line test confirms it is a function since no vertical line intersects it more than once. The horizontal line test also confirms it is one-to-one because no horizontal line intersects the graph at more than one point. This means the linear function is one-to-one.

Finally, for another graph, applying the vertical line test shows it is a function, and the horizontal line test confirms it is one-to-one as well, since no horizontal line intersects the graph more than once.

Understanding these tests is crucial for identifying one-to-one functions, which are important in many areas of mathematics, including inverse functions and function composition. The vertical line test ensures the graph represents a function, while the horizontal line test confirms the function's one-to-one nature, meaning each output corresponds to exactly one input.

Which of the following is the graph of a one-to-one function?

• A.
• B.
• C.
• D.

Answer: (A)

Which of the following is the graph of a one-to-one function?

• A.
• B.
• C.
• D.

Answer: (D)

Consider the following relations. Which is a one-to-one function?

• A. $\left\{(1,4),(2,5),(3,6),(4,7)\right\}$
• B. $\left\{(1,2),(1,3),(2,4)\right\}$
• C. $\left\{\right(2,3),(3,3),(4,5\left)\right\}$
• D. $\left\{\right(1,1),(2,2),(3,1),(9,9\left)\right\}$

Answer: (A)

Intro to Inverse Functions

When a function is one-to-one, it possesses a unique and valuable property: the existence of an inverse function. An inverse function essentially reverses the roles of inputs and outputs of the original function. If the original function is denoted as f, its inverse is written as f⁻¹, where the superscript ⁻¹ indicates the inverse, not an exponent or reciprocal.

For a one-to-one function f with ordered pairs (x, y), the inverse function f⁻¹ consists of ordered pairs (y, x), effectively swapping each input with its corresponding output. This means that if f maps x-values to y-values, then f⁻¹ maps those y-values back to the original x-values.

Consider a function f defined by the ordered pairs (−4, 2), (−2, −1), and (1, 3). Since each output is paired with exactly one input, f is one-to-one and thus has an inverse. The inverse function f⁻¹ will then have the ordered pairs (2, −4), (−1, −2), and (3, 1), reversing the input-output relationship.

This swapping also affects the domain and range. The domain of the original function f (the set of all x-values) becomes the range of the inverse function f⁻¹, while the range of f (the set of all y-values) becomes the domain of f⁻¹. Understanding this relationship is crucial for working with inverse functions and solving problems involving them.

Intro to Inverse Functions Example 2

When determining whether a relation represented by a table of values is a function, the key criterion is that each input corresponds to at most one output. If any input maps to multiple outputs, the relation is not a function. For example, if the input 1 maps to both 4 and 7, this violates the definition of a function. However, if every input has a unique output, the relation qualifies as a function.

To assess if a function is one-to-one (injective), each output must correspond to at most one input. This means no two different inputs share the same output value. For instance, if both inputs 1 and 2 map to the output 4, the function is not one-to-one. When a function is one-to-one, it guarantees the existence of an inverse function, which essentially reverses the mapping of inputs and outputs.

The inverse function, denoted as f⁻¹(x), is found by swapping the inputs and outputs of the original function f(x). In practical terms, if the original function maps input a to output b, then the inverse function maps input b back to output a. This can be represented in a table by interchanging the columns of inputs and outputs. For example, if the original function has pairs (1, 4), (2, 7), (3, 9), and (4, 12), the inverse function will have pairs (4, 1), (7, 2), (9, 3), and (12, 4).

It is important to note that only one-to-one functions have inverses that are also functions. If a function is not one-to-one, meaning some outputs correspond to multiple inputs, then an inverse function does not exist. For example, if the output 10 corresponds to both inputs 2 and 3, the function is not one-to-one, and thus, its inverse cannot be defined as a function.

Consider the set of ordered pairs. Verify if it is one-to-one. If so, find its inverse.
$f=\left\{\right(2,9),(4,11),(6,15),(8,20\left)\right\}$

• A. $f^{-1}=\left\{\right(\frac{1}{9},\frac{1}{2}),(\frac{1}{11},\frac{1}{4}),(\frac{1}{15},\frac{1}{6}),(\frac{1}{20},\frac{1}{8}\left)\right\}$
• B. $f^{-1}=\left\{\right(\frac{1}{2},\frac{1}{9}),(\frac{1}{4},\frac{1}{11}),(\frac{1}{6},\frac{1}{15}),(\frac{1}{8},\frac{1}{20}\left)\right\}$
• C. $f^{-1}=\left\{\right(9,2),(11,4),(15,6),(20,8\left)\right\}$
• D. The function is not one-to-one.

Answer: (C)

Consider the set of ordered pairs. Verify if it is one-to-one. If so, find its inverse.
$g=\left\{\right(1,\frac{3}{2}),(4,\frac{5}{3}),(7,\frac{9}{4}),(10,\frac{11}{6}\left)\right\}$

• A. $g^{-1}=\left\{\right(1,\frac{2}{3}),(\frac{1}{4},\frac{3}{5}),(\frac{1}{7},\frac{4}{9}),(\frac{1}{10},\frac{6}{11}\left)\right\}$
• B. $g^{-1}=\left\{\right(\frac{2}{3},1),(\frac{3}{5},\frac{1}{4}),(\frac{4}{9},\frac{1}{7}),(\frac{6}{11},\frac{1}{10}\left)\right\}$
• C. $g^{-1}=\left\{\right(\frac{3}{2},1),(\frac{5}{3},4),(\frac{9}{4},7),(\frac{11}{6},10\left)\right\}$
• D. The function is not one-to-one.

Answer: (C)

Here’s what students ask on this topic:

What is a one-to-one function and how can I determine if a function is one-to-one?

A one-to-one function is a function where each output value corresponds to exactly one unique input value. This means no two different inputs share the same output. To determine if a function is one-to-one, you can use the horizontal line test on its graph: if any horizontal line intersects the graph at more than one point, the function is not one-to-one. Alternatively, when given ordered pairs, check if any output value repeats for different inputs. If it does, the function is not one-to-one. Understanding this concept is important because only one-to-one functions have inverse functions.

How do I find the inverse of a one-to-one function?

To find the inverse of a one-to-one function, you swap the input and output values. If the original function $f$ has ordered pairs $(x,\; y)$, its inverse $f^\{-1\}$ will have ordered pairs $(y,\; x)$. This means the domain and range of the original function switch roles in the inverse. For example, if $f$ maps $-4$ to $2$, then $f^\{-1\}$ maps $2$ back to $-4$. Remember, the notation $f^\{-1\}$ does not mean the reciprocal of $f$, but the inverse function. Only one-to-one functions have inverses that are also functions.

What is the horizontal line test and why is it important?

The horizontal line test is a graphical method used to determine if a function is one-to-one. You draw horizontal lines across the graph of the function. If any horizontal line intersects the graph at more than one point, the function is not one-to-one. This test is important because only one-to-one functions have inverse functions that are also functions. Passing the horizontal line test ensures that each output corresponds to a unique input, which is necessary for the inverse to exist and be well-defined.

What is the difference between the vertical line test and the horizontal line test?

The vertical line test checks if a graph represents a function by ensuring that no vertical line intersects the graph at more than one point. This confirms that each input has at most one output. The horizontal line test, on the other hand, checks if a function is one-to-one by ensuring that no horizontal line intersects the graph at more than one point. This confirms that each output has at most one input. Both tests are essential: the vertical line test verifies the function property, while the horizontal line test verifies the one-to-one property necessary for inverses.

Why do only one-to-one functions have inverse functions?

Only one-to-one functions have inverse functions because the inverse function reverses the roles of inputs and outputs. For the inverse to be a function, each output of the original function must correspond to exactly one input. If a function is not one-to-one, some outputs correspond to multiple inputs, so swapping inputs and outputs would produce multiple outputs for a single input in the inverse, violating the definition of a function. Therefore, the one-to-one property ensures the inverse is well-defined and is itself a function.