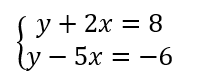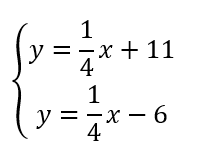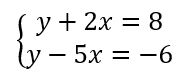Solving Systems of Linear Equations by Graphing: Videos & Practice Problems

Systems of linear equations involve finding $x,y$ pairs that satisfy multiple equations simultaneously. Solutions correspond to the intersection points of lines graphed in slope-intercept form $y=\mathrm{mx}+b$. When slopes differ, there is one unique solution; identical slopes with different intercepts indicate parallel lines and no solution; identical slopes and intercepts mean infinitely many solutions. Checking solutions by substitution ensures accuracy. Understanding these concepts aids in solving multivariable polynomial systems and interpreting polynomial degrees and terms in standard form.

Introduction to Systems of Linear Equations

When working with linear equations, a system of equations refers to a set of two or more equations that are considered simultaneously. Unlike solving a single linear equation, where the solution consists of all the coordinate pairs (x, y) that satisfy that one equation, solving a system of linear equations requires finding the coordinate pairs that satisfy every equation in the system at the same time.

For a single linear equation, such as y = 8x - 4, the solution is represented by all points lying on the line defined by that equation. To determine if a point is a solution, you can either substitute the coordinates into the equation to check if it produces a true statement or graph the point to see if it lies on the line.

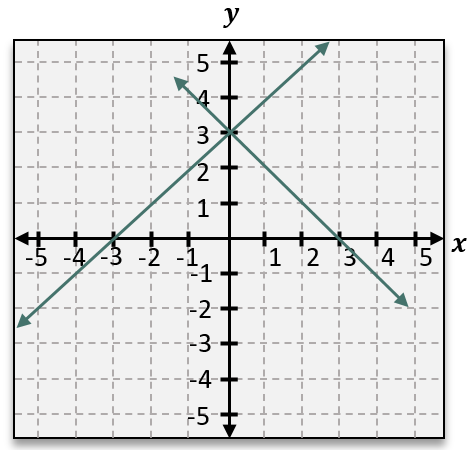
When dealing with a system of linear equations, the solution is the point or points where the graphs of all the equations intersect. This intersection point represents the coordinate pair that satisfies every equation in the system simultaneously. For example, if you have two lines graphed, the solution to the system is the point where these two lines cross. Points that lie on only one of the lines satisfy only one equation and are not solutions to the system.

This concept highlights a key difference: a single linear equation has infinitely many solutions along its line, whereas a system of linear equations typically has a unique solution where the lines intersect. However, some systems may have no solution (if the lines are parallel and never intersect) or infinitely many solutions (if the lines coincide).

Understanding systems of linear equations is fundamental in algebra and is essential for solving real-world problems involving multiple constraints. The graphical interpretation provides a visual way to identify solutions, while algebraic methods allow for precise calculation of the intersection points.

Solve a System of Linear Equations by Graphing

Solving a system of equations by graphing involves finding the point where two or more equations intersect on a coordinate plane. Each equation represents a line, and the solution to the system is the coordinate point that satisfies all equations simultaneously. For example, consider the system:

\(y = x - 3\)

\$3x + y = 5\(

To graph these, first express each equation in slope-intercept form, \)y = mx + b\(, where \)m\( is the slope and \)b\( is the y-intercept. The first equation is already in this form, with a slope of 1 and a y-intercept at -3. Plot the point (0, -3) on the y-axis, then use the slope to find additional points by moving one unit right and one unit up repeatedly.

The second equation, \)3x + y = 5\(, is in standard form. Rearranging it to slope-intercept form gives:

\)y = -3x + 5\(

Here, the slope is -3 and the y-intercept is 5. Start by plotting (0, 5), then use the slope to find other points by moving one unit right and three units down.

After graphing both lines, identify their intersection point, which represents the solution to the system. In this case, the lines intersect at (2, -1). To verify this solution, substitute \)x = 2\( and \)y = -1\( back into both original equations:

For \)y = x - 3\(:

\)-1 \stackrel{?}{=} 2 - 3\(

\)-1 = -1\( (True)

For \)3x + y = 5\(:

\)3(2) + (-1) \stackrel{?}{=} 5\(

\)6 - 1 = 5$ (True)

Since both equations hold true, (2, -1) is the correct solution.

There are other possible outcomes when graphing systems of equations. If the lines are parallel, they never intersect, meaning there is no solution to the system. This occurs when the lines have the same slope but different y-intercepts. Conversely, if the two equations represent the same line, they overlap completely, resulting in infinitely many solutions because every point on the line satisfies both equations.

In summary, solving systems by graphing requires converting equations to slope-intercept form, plotting each line accurately, finding their intersection point, and verifying the solution by substitution. This method visually demonstrates the relationship between equations and their solutions, reinforcing understanding of linear systems.

Use the graph to identify the solution to the system of equations or identify that the system has $0$ or infinitely many solutions. If there is a solution, check that the point satisfies both equations.

• A. $(0,3)$
• B. $(-3,3)$
• C. No Solution
• D. Infinitely many solutions

Answer: (A)

Solve a System of Linear Equations by Graphing Example 1

To solve a system of equations graphically, we need to identify the intersection point where the lines representing the equations cross. In this example, we are given two equations in slope-intercept form: y = 2x + 3 and y = x + 4.

Starting with the first equation, y = 2x + 3, we can determine its graph. The y-intercept is at the point (0, 3), and the slope is 2, indicating that for every 1 unit we move to the right (positive x-direction), we move up 2 units (positive y-direction). Plotting this, we can also move down 2 units and to the left 1 unit to find additional points. Connecting these points gives us the line for this equation.

Next, we analyze the second equation, y = x + 4. Here, the y-intercept is at (0, 4), and the slope is 1, meaning we move up 1 unit and over 1 unit to the right. This line can also be plotted similarly, and connecting the points will yield its graph.

To find the intersection point, we look for where these two lines cross. From the graph, we can see that they intersect at the point (1, 5). This point is crucial as it represents the solution to the system of equations.

To verify that (1, 5) is indeed a solution to both equations, we substitute the x and y values into each equation. For the first equation, substituting gives us:

y = 2x + 3

Substituting x = 1 and y = 5:

5 = 2(1) + 3

5 = 2 + 3

5 = 5, which is a true statement.

Now, we check the second equation:

y = x + 4

Substituting x = 1 and y = 5:

5 = 1 + 4

5 = 5, which is also a true statement.

Since both equations yield true statements when substituting the intersection point (1, 5), we conclude that this point is indeed a solution to the system of equations.

Solve a System of Linear Equations by Graphing Example 2

Solving a system of equations by graphing involves plotting both equations on the coordinate plane and identifying their point of intersection, which represents the solution. When equations are given in standard form, where variables appear on both sides, it is often necessary to convert them into slope-intercept form, expressed as y = mx + b, to facilitate graphing. This form clearly shows the slope m and the y-intercept b, making it easier to plot the line.

To convert from standard form to slope-intercept form, isolate y by moving all x terms to the other side and then dividing by the coefficient of y. For example, starting with an equation like 2x + 6y = -6, subtract 2x from both sides to get 6y = -2x - 6. Then divide every term by 6 to isolate y, resulting in y = -\frac{1}{3}x - 1. This process is repeated for the second equation to ensure both are in slope-intercept form.

When both equations simplify to the same line, such as y = -\frac{1}{3}x - 1, it indicates that the system has infinitely many solutions. This means every point on the line satisfies both equations simultaneously. Graphically, this is represented by the two lines overlapping perfectly, rather than intersecting at a single point.

To graph the line from the slope-intercept form, start at the y-intercept, which is the point where the line crosses the y-axis (in this case, at (0, -1)). Then use the slope, defined as the ratio of the rise over the run, to find additional points. For a slope of -\frac{1}{3}, move down 1 unit and right 3 units from the y-intercept to plot the next point. Connecting these points with a straight line completes the graph.

Understanding the nature of solutions to systems of equations is crucial. If the lines intersect at a single point, there is one unique solution. If the lines are parallel and distinct, there is no solution. However, if the lines coincide, as in this case, there are infinitely many solutions, often described as "infinitely many solutions" or "many solutions." This concept highlights that any point along the overlapping lines satisfies both equations, emphasizing the importance of analyzing the relationship between the equations before graphing.

Solve a System of Linear Equations by Graphing Example 3

In this analysis of systems of equations, we explore how to match equations to their corresponding graphs by utilizing the slope-intercept form, which is expressed as y = mx + b, where m represents the slope and b denotes the y-intercept. This method simplifies the process of identifying the correct graph for each equation.

For the first pair of equations, y = 3x + 5 and y = -2x + 10, we begin by identifying the y-intercepts. The first equation has a y-intercept of 5, while the second has a y-intercept of 10. By examining the graphs, we find that the graph corresponding to y = 3x + 5 intersects the y-axis at 5, confirming its match. The second equation, y = -2x + 10, intersects at 10, aligning with the graph that shows this intersection.

To further validate our matches, we can check the intersection point of the two lines by substituting the coordinates into both equations. For instance, substituting (1, 8) into y = 3x + 5 yields 8 = 3(1) + 5, which simplifies to 8 = 8, confirming the point lies on the line. Similarly, substituting into y = -2x + 10 gives 8 = -2(1) + 10, which also simplifies to 8 = 8.

Next, we analyze the second pair of equations, y = 4x + 8 and another equation with a y-intercept of 10. The first equation has a y-intercept of 8, which we confirm by checking the graphs. The graph that intersects at 8 corresponds to this equation, while the other graph intersects at 10, ruling it out as a match for the first equation.

Finally, we conclude that the third equation, which also has a y-intercept of 10, aligns with the graph that shows this intersection. By rearranging the equations, we can see that both equations share the same y-intercept, further confirming their match with the respective graphs.

This systematic approach to matching equations with their graphs not only reinforces understanding of slope-intercept form but also enhances problem-solving skills in identifying relationships between algebraic expressions and their graphical representations.

Determining Number of Solutions in a System

When analyzing systems of linear equations, the number of solutions can be determined by comparing their slopes and y-intercepts after rewriting each equation in slope-intercept form, \(y = mx + b\). This method allows you to identify whether the system has one solution, no solutions, or infinitely many solutions without graphing.

First, if the slopes (\(m\) values) of the two lines are different, the lines will intersect at exactly one point, meaning the system has a single unique solution. For example, if one equation simplifies to \(y = 0x + 3\) (slope \(m=0\)) and the other to \(y = -1x + 2\) (slope \(m=-1\)), the differing slopes guarantee one solution.

Second, if the slopes are the same but the y-intercepts (\(b\) values) differ, the lines are parallel and will never intersect. This results in zero solutions, indicating an inconsistent system. For instance, \(y = -1x - 1\) and \(y = -1x + 2\) have identical slopes but different intercepts, so no solution exists.

Third, if both the slopes and y-intercepts are identical, the two equations represent the same line. This means there are infinitely many solutions, as every point on the line satisfies both equations. For example, \(y = -1x + 2\) and \(y = -1x + 2\) describe the same line, making the system consistent and dependent.

These scenarios correspond to specific classifications of systems of equations. A system with exactly one solution is called consistent and independent, meaning the equations intersect at a single point and are distinct lines. A system with infinitely many solutions is consistent and dependent, where the equations describe the same line. Lastly, a system with no solutions is inconsistent, as the lines are parallel and never meet.

Understanding how to rewrite equations into slope-intercept form and compare their slopes and intercepts is essential for quickly determining the nature of solutions in linear systems. This approach streamlines problem-solving and deepens comprehension of linear relationships and their graphical interpretations.

Determine the number of solutions the system of equations has without graphing.

• A. $1$
• B. Infinitely Many
• C. $0$

Answer: (A)

Determine the number of solutions the system of equations has without graphing.

• A. $1$
• B. Infinitely Many
• C. $0$

Answer: (C)

Without using a graph, determine the number of solutions in the following systems of equations, then classify the system.

• A. Independent and Consistent
• B. Dependent and Consistent
• C. Inconsistent

Answer: (A)

Here’s what students ask on this topic:

What is the method to solve a system of linear equations by graphing?

To solve a system of linear equations by graphing, first convert each equation into slope-intercept form, which is $y=mx+b$. This form makes it easier to plot the lines on a coordinate plane. Next, plot the y-intercept ($b$) for each line and use the slope ($m$) to find additional points. Draw the lines through these points. The solution to the system is the coordinate pair where the lines intersect, as this point satisfies both equations simultaneously. If the lines intersect at exactly one point, the system has one solution. If the lines are parallel and never intersect, there is no solution. If the lines coincide (are the same line), there are infinitely many solutions. Always check your solution by substituting the intersection point back into the original equations to verify accuracy.

How do you determine the number of solutions in a system of linear equations without graphing?

You can determine the number of solutions by comparing the slopes and y-intercepts of the equations after rewriting them in slope-intercept form ($y=mx+b$). If the slopes ($m$) are different, the lines intersect at one point, so there is exactly one solution. If the slopes are the same but the y-intercepts ($b$) are different, the lines are parallel and never intersect, so there are no solutions. If both the slopes and y-intercepts are identical, the lines coincide, meaning there are infinitely many solutions. This method avoids graphing and relies on algebraic comparison, making it efficient for quickly identifying the nature of the system's solutions.

What are the different types of solutions for systems of linear equations and their meanings?

Systems of linear equations can have three types of solutions: one solution, no solution, or infinitely many solutions. One solution occurs when the lines intersect at a single point; this is called a consistent and independent system. No solution happens when the lines are parallel and never intersect, known as an inconsistent system. Infinitely many solutions occur when the two equations represent the same line, called a consistent and dependent system. Understanding these types helps in analyzing the system's behavior and predicting the number of solutions without graphing.

Why is it important to check the solution of a system of equations after graphing?

Checking the solution after graphing is important because hand-drawn graphs may not be perfectly accurate, leading to incorrect identification of the intersection point. By substituting the coordinates of the intersection point back into the original equations, you verify that the point satisfies both equations, confirming it is a true solution. This step ensures accuracy and helps avoid errors caused by imprecise graphing, especially when the intersection point has fractional or less obvious coordinates.

How do you convert a linear equation from standard form to slope-intercept form for graphing?

To convert a linear equation from standard form ($\mathrm{Ax}+\mathrm{By}=C$) to slope-intercept form ($y=\mathrm{mx}+b$), solve for $y$. For example, given $3x\; +\; y\; =\; 5$, subtract $3x$ from both sides to isolate $y$: $y\; =\; -3x\; +\; 5$. This form reveals the slope ($-3$) and y-intercept ($5$), making it easier to graph the line by plotting the intercept and using the slope to find other points.