Graphing Circles: Videos & Practice Problems

Understanding the standard form of a circle's equation, $x^2-2\mathrm{hx}+y^2-2\mathrm{ky}=r^2$, where h and k represent the center coordinates and r the radius, is essential for graphing circles. Converting from the general form involves completing the square for both x and y terms, transforming polynomials into perfect square trinomials. This process reveals the circle's center and radius, enabling accurate graphing by plotting points at a distance r from the center. Mastery of these algebraic manipulations enhances comprehension of multivariable polynomials and their geometric representations.

Circles in Standard Form

The graph of a circle represents all points equidistant from a fixed point called the center. This fixed distance is known as the radius, typically denoted by r. The center of the circle is given by the ordered pair (h, k), which locates the circle on the coordinate plane. The standard form equation of a circle is expressed as:

\[ (x - h)^2 + (y - k)^2 = r^2 \]

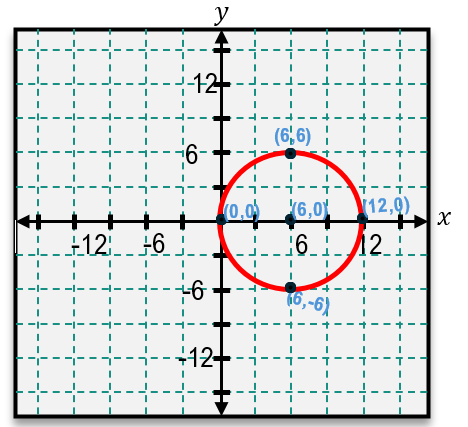
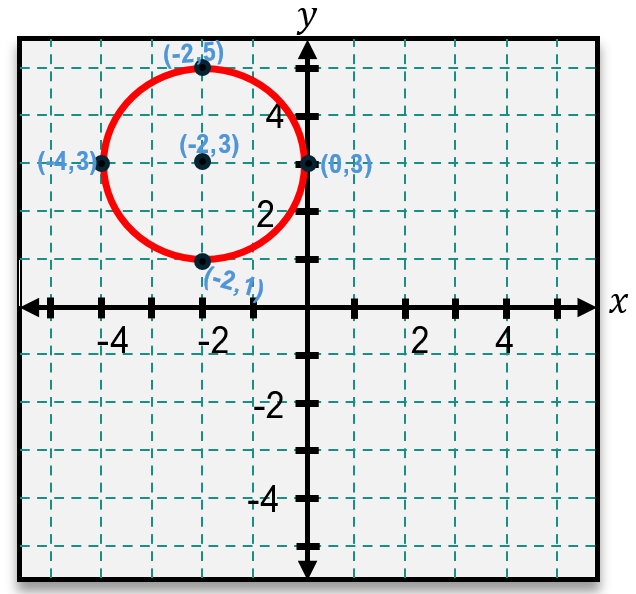
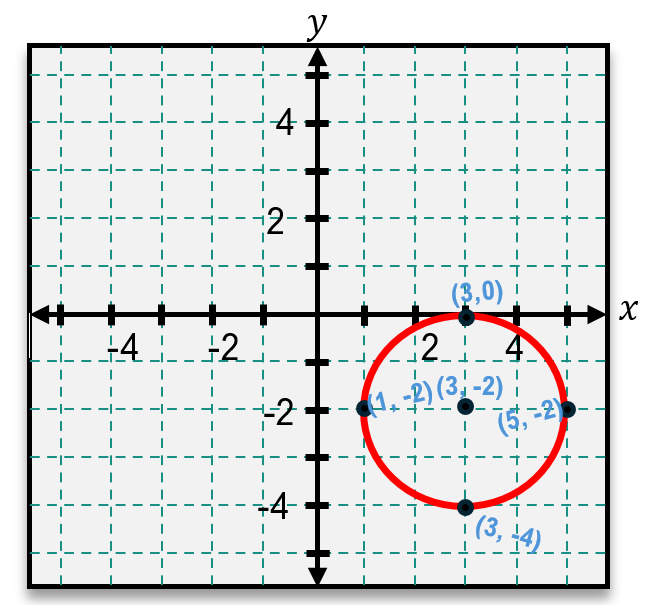
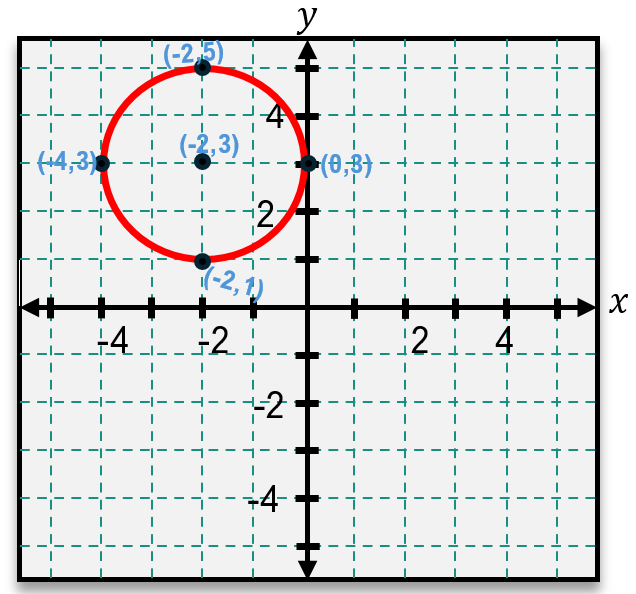
Here, h and k represent the x- and y-coordinates of the center, respectively, while r is the radius. To graph a circle from this equation, first identify the center by interpreting the values of h and k. For example, if the equation contains (x - 2)^2, then h = 2. If it contains (y + 1)^2, remember that this corresponds to y - (-1), so k = -1. The radius is the square root of the constant on the right side of the equation. For instance, if the equation equals 16, then the radius is r = 4 because \$16 = 4^2$.

Once the center and radius are determined, plot the center point on the coordinate plane. From this center, measure the radius length up, down, left, and right to mark four key points. Connecting these points smoothly forms the circle.

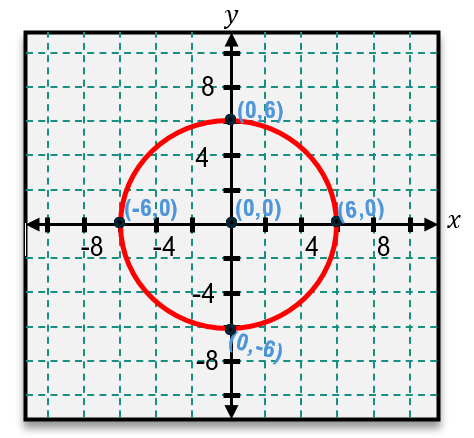
In cases where the circle is centered at the origin (0, 0), the equation simplifies to:

\[ x^2 + y^2 = r^2 \]

This is a special case of the standard form where h = 0 and k = 0, so the terms involving h and k are omitted. Recognizing this form helps quickly identify circles centered at the origin.

Understanding how to interpret and graph circles from their standard form equations is essential for visualizing geometric relationships and solving problems involving circular shapes on the coordinate plane.

Give the center and radius of each circle and graph.
$x^2+y^2=36$

• A. $r=6$; Center: $(6,0)$
• B. $r=6$; Center: $(0,0)$
• C. $r=6$; Center: $(6,0)$
• D. $r=6$; Center: $(0,0)$

Answer: (B)

Give the center and radius of each circle and graph.
$(x+2{)}^2+(y-3{)}^2=4$

• A. $r=2$; Center: $(3,-2)$
• B. $r=2$; Center: $(3,-2)$
• C. $r=2$; Center: $\left(-2,3\right)$
• D. $r=2$; Center: $(-2,3)$
  

Answer: (D)

Circles in Standard Form Example 1

Understanding how to write the equation of a circle from its graph is a fundamental skill in coordinate geometry. The standard form of a circle's equation is given by:

\[ (x - h)^2 + (y - k)^2 = r^2 \]

Here, (h, k) represents the center of the circle, and r is the radius. This form is essential when the circle is not centered at the origin. When the circle is centered at the origin, the equation simplifies to:

\[ x^2 + y^2 = r^2 \]

To write the equation from a graph, first identify the center by locating the coordinates of the circle's midpoint. For example, if the center is at (1, -1), then h = 1 and k = -1. Next, determine the radius by measuring the distance from the center to any point on the circle. If the radius is 4 units, then r = 4.

Substituting these values into the standard form yields:

\[ (x - 1)^2 + (y - (-1))^2 = 4^2 \]

which simplifies to:

\[ (x - 1)^2 + (y + 1)^2 = 16 \]

Similarly, if the center is at (-3, 3) and the radius is 2, the equation becomes:

\[ (x - (-3))^2 + (y - 3)^2 = 2^2 \]

or

\[ (x + 3)^2 + (y - 3)^2 = 4 \]

Mastering this process enhances your ability to interpret and construct equations of circles, deepening your understanding of their geometric properties and their representation in the coordinate plane.

Write the standard form equation of the circle described.
Centered at $(-3,5)$; radius: $7$

• A. ${(x-3)}^2+{(y+5)}^2=49$
• B. ${(-3+x)}^2+{(5+y)}^2=7$
• C. ${(x+3)}^2+{(y-5)}^2=49$
• D. $(x+3)+(y-5)=7$

Answer: (C)

Write the standard form equation of the circle described.
Centered at the origin; diameter: $10$

• A. $x^2+y^2=100$
• B. ${(x-5)}^2+{(y-5)}^2=100$
• C. ${(x-10)}^2+{(y-10)}^2=0$
• D. $x^2+y^2=25$

Answer: (D)

Circles in General Form

In the study of circles, understanding the general form of a circle's equation is crucial for converting it to standard form. The general form of a circle's equation can appear daunting, but with the right approach, it can be simplified. The general form is typically expressed as:

\[x^2 + y^2 + Dx + Ey + F = 0\]

To convert this equation into standard form, which is:

\[ (x - h)^2 + (y - k)^2 = r^2 \]

where \((h, k)\) is the center of the circle and \(r\) is the radius, you will need to complete the square for both the \(x\) and \(y\) terms. The process begins by grouping the \(x\) and \(y\) terms together and moving the constant term to the other side of the equation. For example, if you have:

\[x^2 + 2x + y^2 - 4y + 1 = 0\]

you would rearrange it to:

\[x^2 + 2x + y^2 - 4y = -1\]

Next, you complete the square for the \(x\) terms. Take the coefficient of \(x\) (which is 2), divide it by 2 to get 1, and then square it to add 1. Do the same for the \(y\) terms, where the coefficient is -4. Dividing by 2 gives -2, and squaring it results in 4. You will add these values to both sides of the equation to maintain equality:

\[x^2 + 2x + 1 + y^2 - 4y + 4 = -1 + 1 + 4\]

This simplifies to:

\[ (x + 1)^2 + (y - 2)^2 = 4 \]

Now, you can identify the center of the circle as \((-1, 2)\) and the radius \(r\) as the square root of 4, which is 2. To graph the circle, plot the center and then move 2 units in all directions (up, down, left, right) to find the points on the circle. Finally, connect these points with a smooth curve to complete the circle.

This method of converting from general to standard form and graphing the circle is essential for solving problems related to circles in coordinate geometry.

Write the standard form equation of the circle described. Give the center and radius.
$x^2+y^2-2x+4y-4=0$

• A. ${(x+1)}^2+{(y-2)}^2=3^2$; Center: $(1,-2)$; Radius: $3$
• B. ${(x-1)}^2+{(y+2)}^2=3^2$; Center: $(1,-2)$ ; Radius: $3$
• C. ${(x+1)}^2+{(y-2)}^2=3^2$; Center: $(-1,2)$; Radius: $9$
• D. ${(x-1)}^2+{(y+2)}^2=3^2$; Center: $(-1,2)$; Radius: $3$

Answer: (B)

Write the standard form equation of the circle described. Give the center and radius.
$x^2+y^2-8x-12y+3=0$

• A. ${(x-4)}^2+{(y-6)}^2=7^2$; Center: $(4,6)$; Radius: $7$
• B. $\left(x-4\right)^2+\left(y-6\right)^2=7^2$; Center: $(6,4)$; Radius: $7$
• C. ${(x-6)}^2+{(y-4)}^2=7^2$; Center: $\left(6,4\right)$; Radius: $7$
• D. $\left(x-4\right)^2+\left(y-6\right)^2=7^2$; Center: $\left(4,6\right)$; Radius: $49$

Answer: (A)

Here’s what students ask on this topic:

What is the standard form equation of a circle and how do you identify its center and radius?

The standard form equation of a circle is given by $x^2-2hx+y^2-2ky=r^2$, where (h, k) is the center of the circle and r is the radius. To identify the center and radius from this equation, recognize that h and k are the coordinates of the center point. The radius r is the distance from the center to any point on the circle, and it is the square root of the constant on the right side of the equation. For example, if the equation is $x^2-4x+y^2+6y=12$, you would complete the square to rewrite it in standard form and then identify the center and radius accordingly. Understanding this form is essential for graphing circles accurately.

How do you convert the general form of a circle's equation to standard form?

To convert the general form of a circle's equation, such as $x^2+2x+y^2-4y+1=0$, to standard form, you need to complete the square for both x and y terms. First, group the x terms and y terms separately and move constants to the other side. Then, for each group, take the coefficient of the linear term (b), divide it by 2, and square it. Add this value inside the group and also add it to the other side of the equation to maintain equality. After completing the square, factor each group into a perfect square trinomial. This process reveals the center (h, k) and radius r of the circle in the standard form $x^2-2hx+y^2-2ky=r^2$. This method is crucial for graphing circles from general equations.

How do you graph a circle given its equation in standard form?

To graph a circle from its standard form equation $x^2-2hx+y^2-2ky=r^2$, first identify the center (h, k) by rewriting the equation as $(x\; -h)2^{}+\; (y\; -k)2^{}=\; r{2}^{}$. The center is at point (h, k). The radius r is the square root of the constant on the right side. Plot the center on the coordinate plane, then mark points r units above, below, left, and right of the center. Finally, connect these points smoothly to form the circle. This method ensures an accurate representation of the circle's size and position.

What is the significance of completing the square when working with circle equations?

Completing the square is a vital algebraic technique used to convert the general form of a circle's equation into its standard form. The general form often looks like $x^2+\; bx\; +y^2+\; cy\; +\; d\; =\; 0$, which is not straightforward for identifying the circle's center and radius. By completing the square for both x and y terms, you transform the equation into a form like $(x\; -\; h)2^{}+\; (y\; -\; k)2^{}=\; r{2}^{}$, where (h, k) is the center and r is the radius. This process reveals the geometric properties of the circle, making it easier to graph and understand its position and size on the coordinate plane. Mastery of completing the square is essential for working with circle equations in algebra.

How do you graph a circle centered at the origin?

A circle centered at the origin has its center at (0, 0). Its equation in standard form simplifies to $x^2+y^2=\; r{2}^{}$, where r is the radius. To graph this circle, plot the center at the origin on the coordinate plane. Then, from the origin, mark points r units up, down, left, and right. These points lie on the circle. Finally, connect these points smoothly to form the circle. This method is straightforward because the center is fixed at (0, 0), and the radius directly determines the size of the circle. Understanding this special case helps in quickly graphing circles without needing to complete the square.