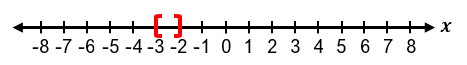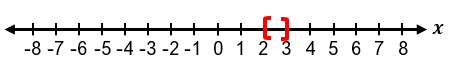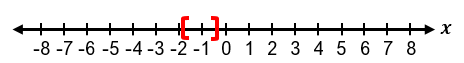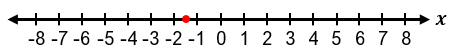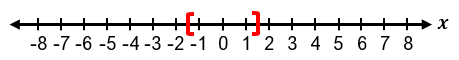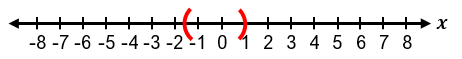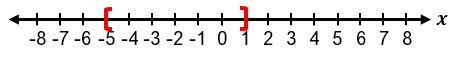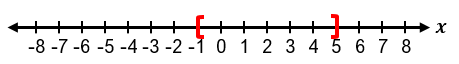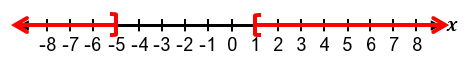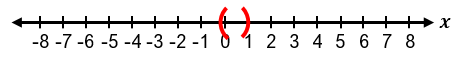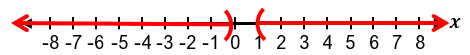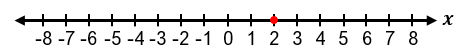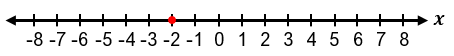Absolute Value Inequalities: Videos & Practice Problems

Solving absolute value inequalities involves isolating the absolute value expression and rewriting it without absolute values. For inequalities like $\mathrm{|x|}<a$, the solution is a three-part inequality $-a<x<a$, representing values between negative and positive $a$. For $\mathrm{|x|}>a$, solutions split into two inequalities: $x>a$ or $x<-a$. Special cases arise when $a$ is zero or negative, reflecting the non-negative nature of absolute values. Solutions can be expressed in interval notation and graphed accordingly.

Solve Absolute Value Inequalities of the Form |X|<a

Solving absolute value inequalities involves combining the techniques used for absolute value equations and inequalities. When faced with an inequality such as |x| < a, it means the distance between x and zero is less than a. This can be rewritten as a compound inequality: −a < x < a. Similarly, if the inequality is |x| ≤ a, it translates to −a ≤ x ≤ a. These forms allow us to solve the inequality by isolating the variable within a three-part inequality.

To solve absolute value inequalities, the first step is to isolate the absolute value expression on one side. For example, in an inequality like |x + 1| + 3 ≤ 5, subtracting 3 from both sides isolates the absolute value, resulting in |x + 1| ≤ 2. This can then be rewritten as the three-part inequality −2 ≤ x + 1 ≤ 2. Solving this involves subtracting 1 from all parts, yielding −3 ≤ x ≤ 1. The solution can be expressed in interval notation as [−3, 1], where brackets indicate that the endpoints are included due to the "less than or equal to" condition. Graphically, this solution is represented by a line segment between −3 and 1 with closed circles at both ends.

It is important to recognize special cases when dealing with absolute value inequalities. Since absolute value represents distance, it cannot be negative. Therefore, if the inequality is of the form |x| < negative number, it has no solution because the absolute value cannot be less than a negative number. If the inequality is |x| ≤ 0, the only solution is when the expression inside the absolute value equals zero, meaning x = 0. For example, if |x + 1| ≤ 0, then x + 1 = 0, so x = −1.

In summary, solving absolute value inequalities with "less than" or "less than or equal to" signs involves isolating the absolute value, rewriting the inequality as a three-part compound inequality, and solving for the variable. Special attention must be given to cases where the boundary value is zero or negative, as these determine whether solutions exist or are unique. Mastery of these steps enables effective solving and interpretation of absolute value inequalities in various mathematical contexts.

Solve and graph the following absolute value inequalities. Express the solution in interval notation.
(A) $\mid \frac{2x-5}{3}\mid \le \frac{1}{3}$

• A. $[-3,-2]$
• B. $(-3,-2)$
• C. $[2,3]$
• D. $(2,3)$

Answer: (C)

Solve and graph the following absolute value inequalities. Express the solution in interval notation.
(B)

• A. $(-4,-1)$
• B. $(1,4)$
• C. $[1,4]$
• D. $[-4,-1]$

Answer: (A)

Solve and graph the following absolute value inequalities.
(A)

• A. All real numbers
• B. $[-1\frac{7}{8},-\frac{3}{8}]$
• C. $(-1\frac{7}{8},-\frac{3}{8})$
• D. No solution

Answer: (D)

Solve and graph the following absolute value inequalities.
(B) $\mid 6x-9\mid -7\le -7$

• A. $x=1.5$
• B. $x=-1.5$
• C. $[-1.5,1.5]$
• D. $(-1.5,1.5)$

Answer: (A)

Solve Absolute Value Inequalities of the Form |X|<a Example 1

Relative error is a key concept used to measure how much an actual value deviates from an expected value, expressed as a fraction of the expected value. It is commonly represented by the formula for relative error:

\[\left| \frac{c - c_t}{c_t} \right| \leq m\]

where c is the actual value, c_t is the target or expected value, and m is the maximum allowable relative error. This inequality ensures that the relative difference between the actual and expected values does not exceed a specified limit.

For example, if a bag of chips is supposed to contain 20 grams but can vary by a relative error of no more than 0.2 (or 20%), the inequality becomes:

\[\left| \frac{c - 20}{20} \right| \leq 0.2\]

To solve this absolute value inequality, rewrite it as a compound inequality:

\[-0.2 \leq \frac{c - 20}{20} \leq 0.2\]

Converting decimals to fractions for easier manipulation, 0.2 equals \(\frac{2}{10}\), so the inequality is:

\[-\frac{2}{10} \leq \frac{c - 20}{20} \leq \frac{2}{10}\]

Multiplying all parts of the inequality by the least common denominator, 20, clears the fractions:

\[20 \times \left(-\frac{2}{10}\right) \leq 20 \times \frac{c - 20}{20} \leq 20 \times \frac{2}{10}\]

Simplifying each term yields:

\[-4 \leq c - 20 \leq 4\]

Adding 20 to all sides isolates c:

\[16 \leq c \leq 24\]

This solution indicates that the actual weight of the chips in each bag can range from 16 grams to 24 grams while maintaining the relative error within the acceptable limit of 0.2. Understanding how to set up and solve absolute value inequalities in the context of relative error is essential for quality control and measurement accuracy in various applications.

Solve Absolute Value Inequalities of the Form |X|>a

Solving absolute value inequalities where the absolute value expression is greater than or greater than or equal to a number involves rewriting the inequality into two separate inequalities without absolute values. This approach builds on the skills used for solving absolute value equations and inequalities. When given an inequality such as \(|x| > a\), it means the distance between \(x\) and zero is greater than \(a\). Therefore, \(x\) must satisfy either \(x > a\) or \(x < -a\). Similarly, for \(|x| \geq a\), the solution set is \(x \geq a\) or \(x \leq -a\). This method requires the absolute value expression to be isolated on one side of the inequality before rewriting.

For example, consider the inequality \(|x + 1| + 3 \geq 5\). The first step is to isolate the absolute value by subtracting 3 from both sides, resulting in \(|x + 1| \geq 2\). Applying the rule, this splits into two inequalities: \(x + 1 \geq 2\) or \(x + 1 \leq -2\). Solving these separately, subtracting 1 from both sides gives \(x \geq 1\) or \(x \leq -3\). The solution set can be expressed in interval notation as \((-\infty, -3] \cup [1, \infty)\), and graphically represented with closed brackets at \(-3\) and \$1\(, extending to negative and positive infinity respectively.

It is important to consider special cases when the number \)a\( is zero or negative. Since absolute value represents distance and is always nonnegative, inequalities like \)|x| \geq 0\( or \)|x| \geq -a\( (where \)a\( is positive) are always true for all real numbers. Thus, the solution set in these cases is all real numbers, \)\mathbb{R}$.

In summary, to solve absolute value inequalities with greater than or greater than or equal to symbols, first isolate the absolute value expression. Then rewrite the inequality as two separate inequalities without absolute values and solve each. If the number on the other side is zero or negative, the solution is all real numbers. This method ensures a clear understanding of how absolute value inequalities describe distances on the number line and how to express their solutions both algebraically and graphically.

Solve and graph the following absolute value inequalities. Express the solution in interval notation.
(A) $\mid 2x+0.6\mid >2.6$

• A. $(-1.6,1)$
• B. $x<-1.6$ OR $x>1$
• C. OR $x>1.6$
• D. $(-1,1.6)$

Answer: (B)

Solve and graph the following absolute value inequalities. Express the solution in interval notation.
(B) $\frac{1}{2}\mid 2x+4\mid +5\ge 8$

• A. $[-5,1]$
• B. $[-1,5]$
• C. OR $x>5$
• D. OR $x>1$

Answer: (D)

Solve and graph the following absolute value inequalities.
(A) $\mid 10x-4\mid -2>-8$

• A. No solution
• B. $(-0.2,1)$
• C. OR $x>1$
• D. All real Numbers

Answer: (D)

Solve and graph the following absolute value inequalities.
(B) $\mid 0.5x+1\mid +8\ge 8$

• A. All real numbers
• B. $x=2$
• C. $x=-2$
• D. No solution

Answer: (A)

Solve Absolute Value Inequalities of the Form |X|>a Example 2

To solve the inequality involving the absolute value expression |3x + 6| > 0, we apply the general rule for absolute value inequalities. Since the inequality is strictly greater than zero, it splits into two separate inequalities: one where the expression inside the absolute value is greater than zero, and another where it is less than zero. This means we consider both 3x + 6 > 0 and 3x + 6 < 0.

Starting with 3x + 6 > 0, subtract 6 from both sides to isolate the term with x:

\$3x > -6\(

Then divide both sides by 3 to solve for x:

\)x > \frac{-6}{3} = -2\(

For the second inequality, 3x + 6 < 0, similarly subtract 6 from both sides:

\)3x < -6\(

Divide both sides by 3:

\)x < \frac{-6}{3} = -2\(

Combining these results, the solution is all real numbers x such that x > -2 or x < -2. This effectively means x can be any real number except -2.

Expressing this solution in interval notation, we exclude -2 by using parentheses (which denote that the endpoint is not included). The solution is the union of two intervals:

\)(-\infty, -2) \cup (-2, \infty)$

Graphically, this is represented by two rays on the number line. At x = -2, open parentheses indicate that -2 is not part of the solution. One ray extends leftward from -2 toward negative infinity, and the other extends rightward from -2 toward positive infinity. This visualization confirms that every real number except -2 satisfies the inequality.

Here’s what students ask on this topic:

How do you solve an absolute value inequality when the absolute value is less than a positive number?

To solve an absolute value inequality of the form $|x|<a$ where $a$ is positive, you rewrite it as a compound inequality without absolute values: $-a<x<a$. This means the value of $x$ lies between $-a$ and $a$. Then, solve the three-part inequality by isolating $x$. For example, if you have $|x+1|<=2$, first isolate the absolute value, then rewrite as $-2<=x+1<=2$. Subtract 1 from all parts to get $-3<=x<=1$. This interval represents the solution set.

What is the method to solve absolute value inequalities when the absolute value is greater than a number?

For inequalities like $|x|>a$ where $a$ is positive, the solution splits into two separate inequalities: $x>a$ or $x<-a$. This means $x$ is either greater than $a$ or less than $-a$. First, isolate the absolute value expression, then rewrite the inequality as two separate inequalities without absolute values. Solve each inequality individually. For example, if $|x+1|>=2$, rewrite as $x+1>=2$ or $x+1<=-2$. Solving these gives $x>=1$ or $x<=-3$.

What special cases should be considered when solving absolute value inequalities?

Special cases arise when the number $a$ in inequalities like $|x|<a$ or $|x|>a$ is zero or negative. Since absolute value represents distance, it cannot be negative. If $a$ is negative in a less than inequality, such as $|x|<-a$, there is no solution because absolute value cannot be less than a negative number. If $a$ is zero in a less than or equal to inequality, the solution is where the expression inside the absolute value equals zero. For greater than or equal to inequalities with $a$ zero or negative, the solution is all real numbers because absolute value is always greater than or equal to zero or any negative number.

How do you express the solution of absolute value inequalities in interval notation and graph form?

After solving an absolute value inequality, express the solution in interval notation and graph it on a number line. For inequalities like $|x|<=a$, the solution is a continuous interval between $-a$ and $a$, written as $[-a,a]$ if inclusive. On the graph, use closed circles or brackets at the endpoints and shade the region between them. For inequalities like $|x|>=a$, the solution consists of two intervals: $(-\infty ,-a]$ and $[a,\infty )$. Graphically, use closed circles at $-a$ and $a$ with arrows extending to negative and positive infinity, respectively.

Why is it important to isolate the absolute value expression before solving absolute value inequalities?

Isolating the absolute value expression on one side of the inequality is crucial because the solving methods rely on rewriting the inequality without absolute values. If the absolute value is not isolated, you cannot correctly apply the rules that convert the absolute value inequality into either a compound inequality (for less than cases) or two separate inequalities (for greater than cases). For example, in $|x+1|+3<=5$, subtracting 3 from both sides isolates the absolute value: $|x+1|<=2$. This step ensures the correct application of the solving rules and avoids errors in the solution process.