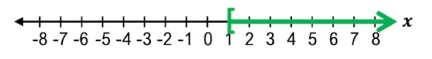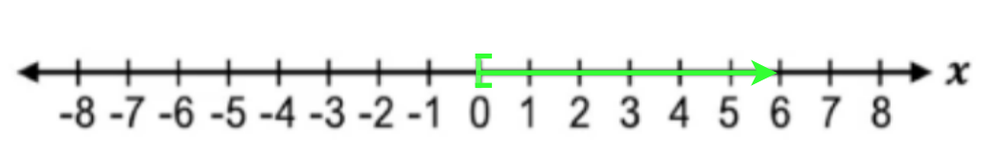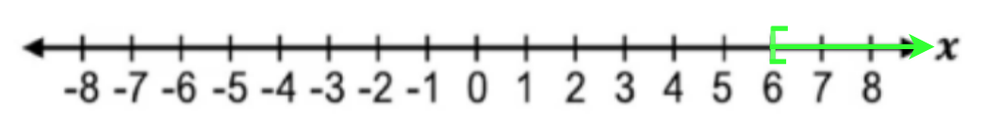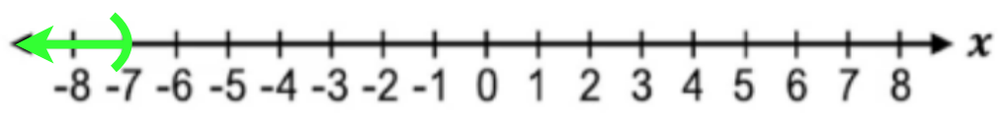Linear Inequalities in One Variable: Videos & Practice Problems

Linear inequalities, expressed as $\mathrm{ax}+b>c$ or with other inequality symbols, have solutions represented by ranges rather than single values. These solutions can be depicted using set builder notation, interval notation, or number lines with parentheses or brackets indicating inclusion or exclusion of boundary points. Solving inequalities involves isolating the variable using addition, subtraction, multiplication, or division, similar to linear equations. However, multiplying or dividing by a negative number requires flipping the inequality symbol to maintain a true statement, ensuring accurate solutions for inequalities involving coefficients and terms.

Introduction to Linear Inequalities

Linear inequalities are closely related to linear equations but differ by using inequality symbols instead of an equal sign. While a linear equation typically takes the form \(ax + b = c\), a linear inequality replaces the equal sign with symbols such as \(>\), \(<\), \(\geq\), or \(\leq\), resulting in expressions like \(ax + b > c\). This subtle change transforms the problem from finding a single solution to identifying a range of solutions.

In a linear equation, solving for \(x\) yields a specific value that satisfies the equation. For example, solving \$2x - 6 = 0\( gives \)x = 3\(. However, when dealing with a linear inequality such as \)2x - 6 > 0\(, the solution is not a single number but all values of \)x\( that make the inequality true. In this case, the solution is \)x > 3\(, meaning any number greater than 3 satisfies the inequality.

To verify solutions of linear inequalities, you can substitute values from the solution range back into the inequality. For instance, plugging in \)x = 5\( into \)2x - 6 > 0\( results in \)2(5) - 6 = 4\(, and since \)4 > 0\( is true, \)x = 5$ is indeed a valid solution. This demonstrates that the solution set of a linear inequality is a continuous range rather than a discrete point.

Understanding linear inequalities involves recognizing their form and interpreting their solutions as ranges of values. This concept builds on the foundation of linear equations, extending problem-solving skills to include inequalities. Mastery of these ideas is essential for graphing inequalities, solving real-world problems, and progressing to more advanced algebraic concepts.

Representing Solutions to Linear Inequalities

When solving inequalities, the solution is not a single value but a range of values. Understanding how to represent and visualize these solution sets is essential. One common way to express inequalities is through set builder notation, which uses curly brackets to define the set of all values that satisfy the inequality. For example, the inequality x > 3 is written as { x | x > 3 }, which reads as "the set of x such that x is greater than 3." The vertical bar means "such that."

Another way to visualize inequalities is on a number line. To represent x > 3, you start at 3 and draw an arrow pointing to the right, indicating all values greater than 3. Since 3 itself is not included, a parenthesis is used at 3 to show exclusion. This use of parentheses to exclude endpoints is consistent with interval notation, where the solution is written as (3, ∞). Here, parentheses around 3 indicate it is not included, and parentheses around infinity are always used because infinity is not a specific number and cannot be included.

For inequalities that include the boundary value, such as x ≥ 3, set builder notation remains similar: { x | x ≥ 3 }. On the number line, the point at 3 is included, so a square bracket or a closed circle is used to indicate inclusion. In interval notation, this is written as [3, ∞), where the square bracket at 3 shows inclusion, and the parenthesis at infinity remains.

When dealing with inequalities where x is less than a value, such as x < 3, the direction of the arrow on the number line points left, toward smaller values. The notation follows the same rules: parentheses indicate exclusion, so the interval notation is (−∞, 3). For x ≤ 3, the interval notation becomes (−∞, 3], with a square bracket indicating that 3 is included.

It is important to remember that in interval notation, infinity and negative infinity always use parentheses because they are not actual numbers and cannot be included in the set. On number lines, open circles represent excluded endpoints, while closed circles represent included endpoints. Although parentheses and square brackets are more commonly used in graphs and interval notation, recognizing open and closed circles is helpful for interpreting inequalities visually.

Mastering these notations—set builder, number line, and interval notation—allows for clear communication and understanding of solution sets for linear inequalities, which is foundational for solving and graphing inequalities effectively.

Which inequality matches the graph?

• A. $x\ge1$
• B. $x\le1$
• C. $x>1$
• D. $x<1$

Answer: (A)

Which inequality matches the graph?

• A. $x\ge1$
• B. $x\le1$
• C. $x>1$
• D. $x<1$

Answer: (A)

Use the number line to graph the following inequality.

$x\ge 6$

• A.
• B.
• C.
• D.

Answer: (C)

Use the number line to graph the following inequality.

$x\ge -7$

• A.
• B.
• C.
• D.

Answer: (A)

Write the following in interval notation.
$x\ge 0$

• A. $\left(-\infty,0\right)$
• B. $\left\lbrack0,\infty\right)$
• C. $\left(0,\infty\right)$
• D. $\left(-\infty,0\right\rbrack$

Answer: (B)

Write the following in interval notation.

• A. $\left(-\infty,7\right\rbrack$
• B. $\left\lbrack7,\infty\right)$
• C. $\left(7,\infty\right)$
• D. $\left(-\infty,7\right)$

Answer: (D)

Rewrite the following as an inequality statement.
$(-\infty ,2]$

• A. $x\le2$
• B. $x<2$
• C. $x\ge2$
• D. $x>2$

Answer: (A)

Rewrite the following as an inequality statement.
$(1,\infty )$

• A. $x\ge1$
• B. $x\le1$
• C. $x>1$
• D. $x<1$

Answer: (C)

Introduction to Linear Inequalities Example 1

Understanding how to translate between inequalities, interval notation, and graphical representations is essential for mastering the concept of inequalities. When given an inequality such as x > -2, it corresponds to the interval notation (-2, ∞), where the parenthesis indicates that -2 is not included in the set. This matches a graph starting just after -2 and extending infinitely to the right.

For inequalities that include the boundary value, such as x ≥ -5, the interval notation uses a square bracket to denote inclusion: [-5, ∞). This means the set includes -5 and all values greater than -5, which is reflected in the graph by a solid point at -5 and an arrow extending to infinity.

Intervals like (4, ∞) represent values greater than 4 but not including 4 itself, indicated by a parenthesis. The corresponding graph starts just after 4 and extends to the right, without including the point at 4.

When dealing with values less than a certain number, such as values less than -2, the interval notation is (-∞, -2), with a parenthesis at -2 to show it is excluded. The graph will have an arrow pointing left from -2, starting just after -2 and extending towards negative infinity.

Intervals that include the endpoint, like (-∞, 3], include all values less than or equal to 3. The square bracket at 3 indicates inclusion, and the graph reflects this with a solid point at 3 and an arrow pointing left towards negative infinity.

It is important to recognize that inequalities can be written in different forms but represent the same set. For example, -1 ≤ x is equivalent to x ≥ -1. The interval notation for this is [-1, ∞), and the graph shows a solid point at -1 with an arrow extending to the right.

By understanding the relationship between inequalities, interval notation, and graphs, one can confidently interpret and convert between these forms. This skill is fundamental in algebra and helps in solving and visualizing inequality problems effectively.

Solving Linear Inequalities

Solving linear inequalities involves isolating the variable using properties similar to those applied in linear equations, but with attention to the inequality symbols. The addition and subtraction properties of inequalities state that if A is greater than B, then adding or subtracting the same value C to both sides preserves the inequality: \(A + C > B + C\) and \(A - C > B - C\). For example, to solve \(x - 3 > 11\), add 3 to both sides to isolate x, resulting in \(x > 14\).

Multiplication and division properties also apply, where multiplying or dividing both sides of an inequality by a positive number maintains the inequality's direction. For instance, if \$2 < \frac{x}{5}\(, multiplying both sides by 5 yields \)10 < x\(. However, a critical distinction arises when multiplying or dividing by a negative number: the inequality symbol must be reversed to maintain a true statement. This is because multiplying or dividing by a negative value changes the sign of each side, necessitating flipping the inequality symbol. For example, solving \)-7x \geq 21\( involves dividing both sides by \)-7\(, which flips the inequality to \)x \leq -3$.

Understanding these properties allows for effective solving of linear inequalities by isolating the variable while carefully managing the inequality direction, especially when negative multiplication or division is involved. This approach ensures accurate solutions and reinforces the foundational connection between solving linear equations and inequalities.

Solving Linear Inequalities Example 2

To solve the linear inequality x + 8 ≤ 12 - x, start by gathering all variable terms on one side and constants on the other. Add x to both sides to eliminate the negative x on the right, resulting in 2x + 8 ≤ 12. Next, subtract 8 from both sides to isolate the variable term: 2x ≤ 4. Finally, divide both sides by 2 to solve for x, giving x ≤ 2.

Graphing this solution on a number line involves marking the point at 2 and shading all values less than or equal to 2. Since the inequality includes equality, use a closed circle or square bracket at 2 to indicate that 2 is part of the solution set.

Expressed in interval notation, the solution is (-∞, 2]. Parentheses are used with infinity because infinity is not a number and cannot be included, while the square bracket at 2 shows that 2 is included in the interval.

This process demonstrates how to solve linear inequalities by applying inverse operations, graph the solution set accurately, and express the solution in interval notation, which is essential for understanding ranges of values that satisfy inequalities.

Solve the following linear inequalities using the addition and subtraction properties of equality.

• A. $x<2$
• B. $x>2$
• C. $x<1.8$
• D. $x\le1.8$

Answer: (A)

Solve the following linear inequalities and write the solution in interval notation.
$2(x+4)\le 3(x-1)+x$

• A. $\frac{11}{2}\ge x$
• B. $\frac{11}{2}\le x$
• C. $\frac{11}{4}\le x$
• D. $\frac{11}{4}\ge x$

Answer: (B)

Solve the following linear inequalities and write the solution in interval notation.

• A. $x<-\frac52$
• B. $x<-\frac{18}{5}$
• C. $x>-\frac{18}{5}$
• D. $x>-\frac52$

Answer: (C)

Solving Linear Inequalities Example 3

When solving inequalities, it is important to isolate the variable terms on one side and the constants on the other. Consider the inequality \$2x - 5 < 2x + 10\(. By subtracting \)2x\( from both sides, the variable terms cancel out, leaving \)-5 < 10\(. Since this statement is always true, the inequality holds for all real numbers. This means the solution set includes every real number because no matter what value of \)x\( is substituted, the inequality remains valid.

In contrast, examine the inequality \)x + 2 \geq x + 8\(. Subtracting \)x\( from both sides eliminates the variable terms, resulting in \)2 \geq 8\(. This is a false statement, indicating that the inequality has no solution. Such inequalities are called inconsistent because no value of \)x$ can satisfy them.

These examples illustrate key concepts in solving linear inequalities. When variables cancel and the resulting statement is true, the solution is all real numbers, reflecting an identity inequality. When variables cancel and the resulting statement is false, the inequality is inconsistent, meaning no solution exists. Understanding these outcomes helps in analyzing inequalities effectively and recognizing when solutions are universal or nonexistent.

Here’s what students ask on this topic:

What is a linear inequality and how does it differ from a linear equation?

A linear inequality is similar to a linear equation but instead of an equal sign, it uses inequality symbols such as >, <, ≥, or ≤. For example, a linear equation looks like $\mathrm{2x}-6=0$, while a linear inequality might be $\mathrm{2x}-6>0$. The key difference is that the solution to a linear equation is a single value of $x$ that makes the equation true, whereas the solution to a linear inequality is a range of values that satisfy the inequality. For example, $x=3$ solves the equation, but $x>3$ represents all values greater than 3 that satisfy the inequality.

How do you represent the solution of a linear inequality using interval notation?

Interval notation is a concise way to represent the range of solutions to a linear inequality. For example, if the solution is $x>3$, the interval notation is $(3,\infty )$, where parentheses indicate that 3 is not included. If the inequality is $x\ge 3$, the notation is $[3,\infty )$, using a square bracket to show inclusion of 3. Infinity is always represented with a parenthesis because it is not a finite number and cannot be included. Similarly, for inequalities like $x<3$, the interval is $(-\infty ,3)$, and for $x\le 3$, it is $(-\infty ,3]$.

What happens to the inequality symbol when multiplying or dividing both sides of a linear inequality by a negative number?

When you multiply or divide both sides of a linear inequality by a negative number, you must reverse the direction of the inequality symbol to maintain a true statement. For example, if you have $-7x\ge 21$ and divide both sides by $-7$, the inequality symbol flips from ≥ to ≤, resulting in $x\le -3$. This flip is necessary because multiplying or dividing by a negative number reverses the order of the values. Forgetting to flip the inequality symbol leads to incorrect solutions.

How can you graphically represent the solution of a linear inequality on a number line?

To graph the solution of a linear inequality on a number line, first identify the boundary value. For example, for $x>3$, place an open circle at 3 to indicate that 3 is not included. Then draw an arrow extending to the right to represent all values greater than 3. If the inequality is inclusive, like $x\ge 3$, use a closed circle or square bracket at 3 to show inclusion, and draw the arrow to the right. For inequalities with < or ≤, the arrow points to the left. Parentheses and brackets are used in interval notation to correspond with open and closed circles on the graph.

What are the steps to solve a linear inequality?

Solving a linear inequality involves isolating the variable using similar steps as solving linear equations. First, use addition or subtraction to eliminate constants on the variable's side. For example, if you have $x-3>11$, add 3 to both sides to get $x>14$. Next, use multiplication or division to remove coefficients. If multiplying or dividing by a positive number, keep the inequality symbol the same. However, if multiplying or dividing by a negative number, flip the inequality symbol. For example, dividing $-7x\; \ge \; 21$ by $-7$ flips the symbol to get $x\; 64;\; -3$. Always perform the same operation on both sides and remember to flip the inequality when multiplying or dividing by negatives.