14. Conic Sections & Systems of Nonlinear Equations

Ellipses

14. Conic Sections & Systems of Nonlinear Equations

Ellipses: Videos & Practice Problems

Topic summary

An ellipse is an oval shape defined by points where the sum of distances to two foci is constant, contrasting with a circle's single-radius distance. Its equation resembles a circle's but includes two distances: $x^{2} / a^{2} + y^{2} / b^{2} = 1$ , where $a$ and $b$ represent horizontal and vertical distances. Graphing involves plotting points $a$ units left/right and $b$ units up/down from the center, highlighting the importance of understanding terms like radius, foci, and standard form in polynomial expressions.

concept

Ellipses At The Origin

Video duration:

Ellipses At The Origin Video Summary

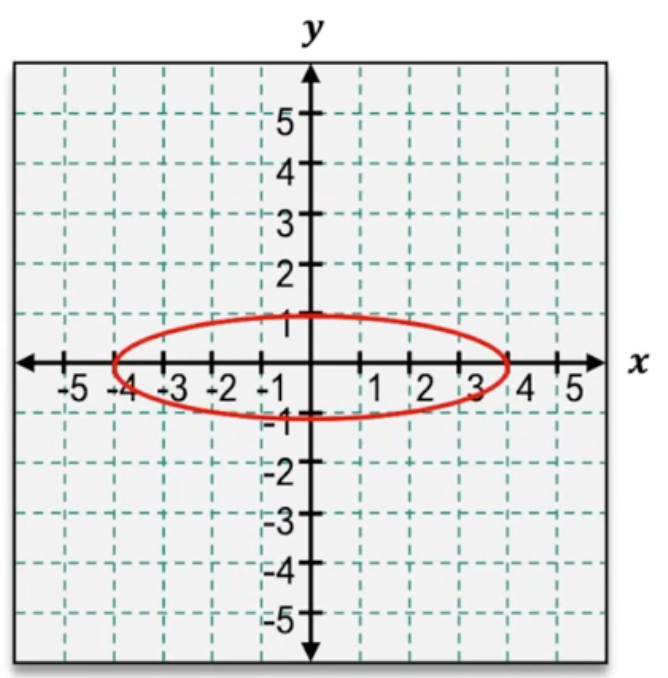
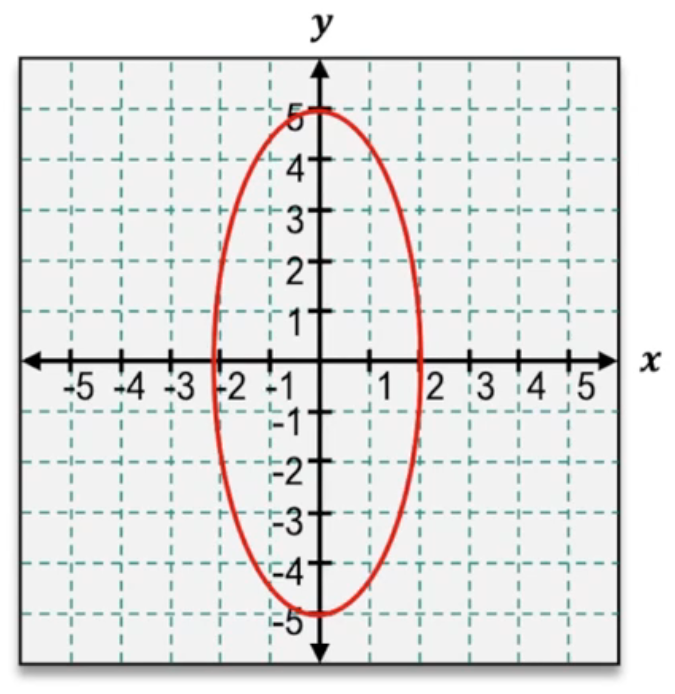
An ellipse is a geometric shape closely related to a circle but with distinct properties. While a circle consists of all points equidistant from a single center point, an ellipse is defined as the set of all points where the sum of the distances to two fixed points, called the foci, remains constant. This difference means that instead of a single radius, an ellipse involves two key distances that determine its shape.

Ellipses can be oriented either vertically or horizontally. In a vertically stretched ellipse, the foci lie along the y-axis, and the ellipse extends further in the vertical direction. Conversely, in a horizontally stretched ellipse, the foci are positioned along the x-axis, and the ellipse stretches more along the horizontal direction. The two main parameters that describe an ellipse are a and b, representing the distances from the center to the ellipse along the major and minor axes, respectively. For a vertical ellipse, b is the longer distance (vertical stretch), and a is the shorter (horizontal). For a horizontal ellipse, a is the longer distance (horizontal stretch), and b is the shorter (vertical).

The standard equation of an ellipse centered at the origin reflects these distances and is similar in form to the equation of a circle. The equation is given by:

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\]

Here, a and b are the lengths of the semi-major and semi-minor axes, respectively. This equation generalizes the circle's equation, which is a special case where a equals b, representing the radius. For example, if an ellipse is vertically stretched with a = 3 and b = 4, its equation becomes:

\[\frac{x^2}{9} + \frac{y^2}{16} = 1\]

For a horizontally stretched ellipse with a = 4 and b = 3, the equation is:

\[\frac{x^2}{16} + \frac{y^2}{9} = 1\]

When graphing an ellipse centered at the origin, the process involves plotting points a units to the right and left along the x-axis and b units up and down along the y-axis. Connecting these points with a smooth, oval curve forms the ellipse. Understanding the relationship between the ellipse’s foci, axes, and equation is essential for accurately sketching and analyzing ellipses in coordinate geometry.

Problem

Write the standard form equation of each ellipse centered at the origin.

$\frac{x^{2}}{4} + y^{2} = 1$

$x^{2} + \frac{y^{2}}{16} = 1$

$x^{2} + y^{2} = 16$

$\frac{x^{2}}{16} + y^{2} = 1$

Problem

Write the standard form equation of each ellipse centered at the origin.

$\frac{x^{2}}{4} + \frac{y^{2}}{25} = 1$

$\frac{x^{2}}{25} + \frac{y^{2}}{4} = 1$

$\frac{x^{2}}{2} + \frac{y^{2}}{5} = 1$

$\frac{x^{2}}{5} + \frac{y^{2}}{2} = 1$

example

Ellipses At The Origin Example 1

Video duration:

Ellipses At The Origin Example 1 Video Summary

To find the x- and y-intercepts of an ellipse and graph it, start by recalling that the x-intercepts occur where y = 0, and the y-intercepts occur where x = 0. Given the ellipse equation, setting y = 0 simplifies the equation because all terms involving y vanish. For example, if the ellipse equation is of the form $\frac{x^2}{16} + \frac{y^2}{25} = 1$, substituting y = 0 reduces it to $\frac{x^2}{16} = 1$. Multiplying both sides by 16 yields $x^2 = 16$, and taking the square root gives $x = \pm 4$. Thus, the x-intercepts are at (4, 0) and (-4, 0).

Next, to find the y-intercepts, set x = 0. This simplifies the equation to $\frac{y^2}{25} = 1$. Multiplying both sides by 25 results in $y^2 = 25$, and taking the square root gives $y = \pm 5$. Therefore, the y-intercepts are at (0, 5) and (0, -5).

Since the ellipse is centered at the origin, these intercepts indicate the ellipse stretches 4 units left and right along the x-axis and 5 units up and down along the y-axis. Plotting these points on the coordinate plane provides key reference points for the ellipse.

To graph the ellipse, connect these intercept points smoothly, forming an oval shape. This curve represents all points satisfying the ellipse equation. The process highlights how the denominators in the ellipse equation correspond to the squares of the intercept distances along each axis, reflecting the ellipse's width and height.

Understanding how to find intercepts and graph ellipses is fundamental in coordinate geometry, enabling visualization of conic sections and their properties.

example

Ellipses At The Origin Example 2

Video duration:

Ellipses At The Origin Example 2 Video Summary

To graph an ellipse given by an equation that is not initially in standard form, it is essential to first rewrite the equation to match the standard ellipse equation centered at the origin:
$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $.

When the equation has a constant other than 1 on the right side, such as 36, divide both sides of the equation by that constant to normalize it. For example, dividing both sides by 36 transforms the equation into a form where the right side equals 1. This step is crucial because the standard form requires the right side to be 1 for easy identification of the ellipse's parameters.

Next, simplify the coefficients of $x^2$ and $y^2$ by factoring and canceling common factors. For instance, if the coefficients are multiples of 4 and 9, factor these out to rewrite the equation as:
$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $.

From this form, identify $a^2$ and $b^2$ directly. Here, $a^2 = 9$ and $b^2 = 4$. Taking the square roots gives the ellipse's semi-major and semi-minor axes:
$a = \sqrt{9} = 3$ and $b = \sqrt{4} = 2$.

Since the ellipse is centered at the origin, plot points at distances $a$ and $b$ along the x- and y-axes respectively. This means marking points 3 units to the left and right of the origin, and 2 units above and below the origin. Connecting these points smoothly forms the characteristic oval shape of the ellipse.

This method highlights the importance of transforming any ellipse equation into its standard form to easily determine its dimensions and graph it accurately. By normalizing the equation and extracting $a$ and $b$, one can confidently plot the ellipse even when the initial equation appears complex.

Here’s what students ask on this topic:

An ellipse is an oval-shaped curve defined as the set of all points where the sum of the distances to two fixed points, called foci, is constant. This contrasts with a circle, which is the set of points equidistant from a single center point. In a circle, every point on the edge is the same distance (radius) from the center. In an ellipse, the sum of distances from any point on the curve to the two foci remains constant, but the individual distances vary. This difference results in the ellipse having two axes of symmetry, a major axis and a minor axis, unlike the circle which has equal radii in all directions.

The standard equation of an ellipse centered at the origin depends on its orientation. For a horizontal ellipse, the equation is $x^{2} / a^{2} + y^{2} / b^{2} = 1$ , where $a$ is the length of the semi-major axis along the x-axis and $b$ is the length of the semi-minor axis along the y-axis. For a vertical ellipse, the roles of $a$ and $b$ switch: $x^{2} / b^{2} + y^{2} / a^{2} = 1$ . Here, $a$ is the longer distance from the center to the ellipse edge, and $b$ is the shorter distance.

To graph an ellipse centered at the origin, first identify the values of $a$ and $b$ from the equation $x^{2} / a^{2} + y^{2} / b^{2} = 1$ . Then, plot points $a$ units to the right and left of the center (along the x-axis) and $b$ units up and down (along the y-axis). Connect these points smoothly to form the ellipse. The longer distance corresponds to the major axis, and the shorter to the minor axis. This method is similar to graphing a circle but accounts for the ellipse's stretched shape.

The foci (singular: focus) of an ellipse are two fixed points located along the major axis inside the ellipse. The defining property of an ellipse is that for any point on the ellipse, the sum of the distances to these two foci is constant. This property distinguishes ellipses from circles, which have a single center point. The foci help determine the shape and orientation of the ellipse. Knowing the foci is essential for understanding the ellipse's geometry and for applications such as planetary orbits, where the path of a planet is an ellipse with the sun at one focus.

The values $a$ and $b$ represent the distances from the center to the ellipse along the major and minor axes, respectively. If $a$ is greater than $b$ , the ellipse is stretched more along the axis corresponding to $a$ , making it elongated. If $a$ equals $b$ , the ellipse becomes a circle. The larger the difference between $a$ and $b$ , the more elongated the ellipse appears. Thus, these values control the ellipse's width and height and determine its overall shape.