Graphs and Graphing
Graph the curves in Exercises 33–42.
y = 𝓍³ (8―𝓍 )
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: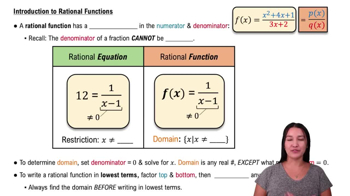


 11:41m
11:41mMaster Summary of Curve Sketching with a bite sized video explanation from Patrick
Start learning