Multiple Choice
In a right triangle, angle is acute. The side opposite has length , the side adjacent to has length , and the hypotenuse has length . Which expressions give and ?
9
views
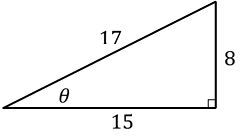
cosθ=178
cosθ=158
cosθ=1715
cosθ=815
 Verified step by step guidance
Verified step by step guidance