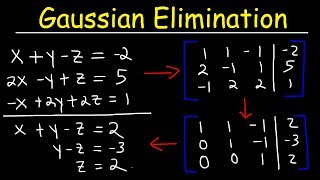
7. Systems of Equations & Matrices

Introduction to Matrices

7. Systems of Equations & Matrices

Introduction to Matrices

Guided videos.

Learn with Patrick

Go to the course

Guided course

4:35

Introduction to Matrices

Performing Row Operations on Matrices

Solving Systems of Equations - Matrices (Row-Echelon Form)

Solving Systems of Equations - Matrices (Reduced Row-Echelon Form)

Showing 6 of 6 videos

Additional 2 creators.

Learn with other creators

Multiplying Matrices - Example 2

Gaussian Elimination with Back Substitution

Mario's Math Tutoring

245

views

Solve linear systems using Gaussian elimination with back substitution

06:33

Solve linear systems using Gaussian elimination with back substitution

Gaussian Elimination & Row Echelon Form

The Organic Chemistry Tutor

479

views

❤︎² Gaussian Elimination.. How? (mathbff)

09:54

❤︎² Gaussian Elimination.. How? (mathbff)

Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 2

Inverse Matrix Using Gauss-Jordan / Row Reduction, Example 1

Inverse Matrix Using Gauss-Jordan / Row Reduction, Example 2

patrickJMT

266

views

Showing 9 of 9 videos

Practice this topic

Multiple Choice

Write the equations in standard form, then represent the system using an augmented matrix.

$3x+5y-9=0$

$8x=-4y+3$

views

Has a video solution.

Multiple Choice

Perform the indicated Row Operation.

SWAP $R_1\leftrightarrow R_2$

views

Has a video solution.

Multiple Choice

Perform the indicated Row Operation.

ADD $R_1+2\cdot R_3\rightarrow R_1$

views

Has a video solution.

Multiple Choice

Solve the system of equations by using row operations to write a matrix in REDUCED row-echelon form.

$4x+2y+3z=6$

$x+y+z=3$

$5x+y+2z=5$

views

Has a video solution.

Multiple Choice

Write the system of equations represented by the augmented matrix shown.

views

Has a video solution.

Textbook Question

In Exercises 1–8, write the augmented matrix for each system of linear equations.

109

views

Has a video solution.

Textbook Question

In Exercises 1–2, perform each matrix row operation and write the new matrix.

401

views

Has a video solution.

Textbook Question

How many rows and how many columns does this matrix have? What is its dimension? <4x2 Matrix>

views

Has a video solution.

Textbook Question

In Exercises 1 - 4, a. Give the order of each matrix, b. If A = [a_ij], identify a_32 and a_23, or explain why identification is not possible, 4 - 7 5 - 6 8 - 1 (please enclose the values above in a matrix symbol)

109

views

Has a video solution.

Textbook Question

In Exercises 1–8, write the augmented matrix for each system of linear equations.

117

views

Has a video solution.

Textbook Question

In Exercises 3–5, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

277

views

Has a video solution.

Textbook Question

What is the augmented matrix of the following system? -3x + 5y = 2 6x + 2y = 7

105

views

Has a video solution.

Textbook Question

In Exercises 3–5, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

202

views

Has a video solution.

Textbook Question

In Exercises 3–5, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

132

views

Has a video solution.

Textbook Question

In Exercises 1–8, write the augmented matrix for each system of linear equations.

162

views

Has a video solution.

Textbook Question

Use the given row transformation to change each matrix as indicated. See Sample 1. < 2x2 Matrix > ; -4 times row 1 added to row 2

105

views

Has a video solution.

Textbook Question

In Exercises 1–8, write the augmented matrix for each system of linear equations.

120

views

Has a video solution.

Textbook Question

Use the given row transformation to change each matrix as indicated. See Sample 1. < 2x2 Matrix > ; -7 times row 1 added to row 2

views

Has a video solution.

Textbook Question

In Exercises 9-12, write the system of linear equations represented by the augmented matrix. Use x, y, and z, or, if necessary, w, x, y, and z, for the variables.

104

views

Has a video solution.

Textbook Question

Use the given row transformation to change each matrix as indicated. See Sample 1. < 3x3 Matrix > ; 2 times row 1 added to row 2

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: b. A - B 4 1 5 9 A = B = 3 2 0 7

views

Has a video solution.

Textbook Question

Find the dimension of each matrix. Identify any square, column, or row matrices. See the discussion preceding Example 1.

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: d. - 3A + 2B 4 1 5 9 A = B = 3 2 0 7

views

Has a video solution.

Textbook Question

Use the given row transformation to change each matrix as indicated. See Sample 1. < 3x3 Matrix > ; 4 times row 1 added to row 2

views

Has a video solution.

Textbook Question

In Exercises 9-12, write the system of linear equations represented by the augmented matrix. Use x, y, and z, or, if necessary, w, x, y, and z, for the variables.

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: a. A + B 3 1 1 2 - 3 6 A = B = - 1 2 5 - 3 1 - 4

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: d. - 3A + 2B 3 1 1 2 - 3 6 A = B = - 1 2 5 - 3 1 - 4

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: c. - 4A 3 1 1 2 - 3 6 A = B = - 1 2 5 - 3 1 - 4

views

Has a video solution.

Textbook Question

Write the augmented matrix for each system and give its dimension. Do not solve. 2x + y + z - 3 = 0 3x - 4y + 2z + 7 = 0 x + y + z - 2 = 0

views

Has a video solution.

Textbook Question

In Exercises 13–18, perform each matrix row operation and write the new matrix.

105

views

Has a video solution.

Textbook Question

Write the augmented matrix for each system and give its dimension. Do not solve. 4x - 2y + 3z - 4 = 0 3x + 5y + z - 7 = 0 5x - y + 4z - 7 = 0

views

Has a video solution.

Textbook Question

In Exercises 14–27, perform the indicated matrix operations given that and D are defined as follows. If an operation is not defined, state the reason. A+D

108

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: a. A + B A = [6 2 - 3], B = [4 - 2 3]

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: c. - 4A A = [6 2 - 3], B = [4 - 2 3]

112

views

Has a video solution.

Textbook Question

In Exercises 13–18, perform each matrix row operation and write the new matrix.

views

Has a video solution.

Textbook Question

Write the system of equations associated with each augmented matrix . Do not solve. <4x3 Matrix>

views

Has a video solution.

Textbook Question

In Exercises 9 - 16, find the following matrices: d. - 3A + 2B 2 - 10 - 2 6 10 - 2 A = 14 12 10 B = 0 - 12 - 4 4 - 2 2 - 5 2 - 2

views

Has a video solution.

Textbook Question

In Exercises 14–27, perform the indicated matrix operations given that and D are defined as follows. If an operation is not defined, state the reason. D-A

116

views

Has a video solution.

Textbook Question

In Exercises 13–18, perform each matrix row operation and write the new matrix.

views

Has a video solution.

Textbook Question

Write the system of equations associated with each augmented matrix . Do not solve. <4x3 Matrix>

views

Has a video solution.

Textbook Question

In Exercises 14–27, perform the indicated matrix operations given that and D are defined as follows. If an operation is not defined, state the reason. 3A+2D

164

views

Has a video solution.

Textbook Question

In Exercises 19–20, a few steps in the process of simplifying the given matrix to row-echelon form, with 1s down the diagonal from upper left to lower right, and 0s below the 1s, are shown. Fill in the missing numbers in the steps that are shown.

155

views

Has a video solution.

Textbook Question

Write the system of equations associated with each augmented matrix . Do not solve.

views

Has a video solution.

Textbook Question

Find the values of the variables for which each statement is true, if possible. See Examples 1 and 2. =

views

Has a video solution.

Textbook Question

In Exercises 17 - 26, let - 3 - 7 - 5 - 1 A = 2 - 9 and B = 0 0 5 0 3 - 4 Solve each matrix equation for X. 2X + A = B

views

Has a video solution.

Textbook Question

In Exercises 14–27, perform the indicated matrix operations given that and D are defined as follows. If an operation is not defined, state the reason. -5(A+D)

153

views

Has a video solution.

Textbook Question

Use the Gauss-Jordan method to solve each system of equations. For systems in two variables with infinitely many solutions, write the solution with y arbitrary. For systems in three variables with infinitely many solutions, write the solution set with z arbitrary. See Examples 1-4. x + y = 5 x - y = -1

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

141

views

Has a video solution.

Textbook Question

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

145

views

Has a video solution.

Textbook Question

In Exercises 14–27, perform the indicated matrix operations given that and D are defined as follows. If an operation is not defined, state the reason. BD

185

views

Has a video solution.

Textbook Question

Solve each system, using the method indicated. 5x + 2y = -10 3x - 5y = -6 (Gauss-Jordan)

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

143

views

Has a video solution.

Textbook Question

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

views

Has a video solution.

Textbook Question

134

views

Has a video solution.

Textbook Question

Solve each system, using the method indicated. 3x + y = -7 x - y = -5 (Gaussian elimination)

views

Has a video solution.

Textbook Question

Solve for X in the matrix equation 3X+A = B where

232

views

Has a video solution.

Textbook Question

views

Has a video solution.

Textbook Question

Solve each system, using the method indicated. x - z = -3 y + z = 6 2x - 3z = -9 (Gauss-Jordan)

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

views

Has a video solution.

Textbook Question

In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 1 2 A = [1 2 3 4], B = 3 4

views

Has a video solution.

Textbook Question

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

105

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

243

views

Has a video solution.

Textbook Question

In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 4 2 2 3 4 A = 6 1 B = 3 5 - 1 - 2 0

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

views

Has a video solution.

Textbook Question

In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.

views

Has a video solution.

Textbook Question

Find the quadratic function f(x) = ax² + bx + c for which ƒ( − 2) = −4, ƒ(1) = 2, and f(2) = 0.

141

views

Has a video solution.

Textbook Question

Find each sum or difference, if possible. See Examples 2 and 3. <1x4 Matrix> - <1x4 Matrix>

views

Has a video solution.

Textbook Question

Find the cubic function f(x) = ax³ + bx² + cx + d for which ƒ( − 1) = 0, ƒ(1) = 2, ƒ(2) = 3, and ƒ(3) = 12.

views

Has a video solution.

Textbook Question

Solve the system: (Hint: Let A = ln w, B = ln x, C = ln y, and D = ln z. Solve the system for A, B, C, and D. Then use the logarithmic equations to find w, x, y, and z.)

105

views

Has a video solution.

Textbook Question

In Exercises 37 - 44, perform the indicated matrix operations given that A, B and C are defined as follows. If an operation is not defined, state the reason. 4 0 5 1 1 - 1 A = - 3 5 B = C = 0 1 - 2 - 2 - 1 1 A(BC)

123

views

Has a video solution.

Textbook Question

Let A = and B = . Find each of the following. See Examples 2 –4. (3/2)B

views

Has a video solution.

Textbook Question

Find each product, if possible. See Examples 5–7. <4x2 Matrix>

views

Has a video solution.

Textbook Question

Find the values of the variables for which each statement is true, if possible. [2x2 matrix] = [2x2 matrix]

views

Has a video solution.

Showing 76 of 76 practice

My Channels

Chemistry

Biology

Math

Physics

Business

Social Sciences

Programming

Product & Marketing

7. Systems of Equations & Matrices

Introduction to Matrices

Learn with Patrick

Learn with other creators

Practice this topic